Алгебра: Найти производную сложной функции у=f(x)

Найти производную сложной функции у=f(x)

👇

Ответ:

БЕЙТУЛЛА

22.01.2020

$y=arccos(ln\sqrt[3]{x})\\\\y'=-\frac{1}{\sqrt{1-(ln\sqrt[3]{x})^2}}\cdot (ln\sqrt[3]{x})'=-\frac{1}{\sqrt{1-ln^2\sqrt[3]{x}}}\cdot \frac{1}{\sqrt[3]{x}}\cdot \frac{1}{3}\cdot x^{-\frac{2}{3}}=\\\\=-\frac{1}{\sqrt{1-ln^2\sqrt[3]{x}}}\cdot \frac{1}{3x}$

4,7(34 оценок)

Открыть все ответы

Ответ:

youyousiis

22.01.2020

Объяснение:

Системы линейных уравнений решаются тремя

1) Методом подстановки;

2) Методом сложения;

3) Графическим методом.

Мы будем решать системы сложения.

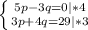
$\left \{ {{5p - 3q = 0 | * 4} \atop {3p + 4q = 29 |*3}} \right.$

Первое уравнение мы домножим на 4, второе - на 3.

Мы домножаем уравнения для того, чтобы уравнять переменные. (Иначе мы не решим систему).

Получим обновленную систему уравнений:

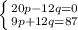
$\left \{ {{20p - 12q = 0} \atop {9p + 12q = 87}} \right.$

12q и -12q взаимно уничтожатся с сложения. Остальные переменные тоже складываются.

В итоге имеем:

29p = 87

p = 3

Мы нашли значение переменной p. Переписываем это значение и берем одно из уравнений системы, которая была у нас сначала:

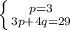
$\left \{ {{p = 3} \atop {3p + 4q = 29}} \right.$

Я взял выражение 3p + 4q потому, что здесь все знаки положительные.

Подставляем значение p:

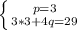
$\left \{ {{p = 3} \atop {3 * 3 + 4q = 29}} \right.$

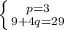
$\left \{ {{p = 3} \atop {9 + 4q = 29}} \right.$

Имеем:

4q = 20

q = 5

Система №2.

(Попробуй решить самостоятельно).

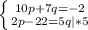
$\left \{ {{10p +7q = -2} \atop {2p - 22 = 5q |*5}} \right. \\$

Домножаем второе уравнение на 5.

Имеем:

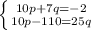
$\left \{ {{10p + 7q = -2} \atop {10p - 110 = 25q}} \right.$

-110 переносим вправо, 25q - влево.

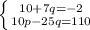
$\left \{ {{10 + 7q = -2} \atop {10p - 25q = 110}} \right.$

10p уничтожится вычитанием. Следовательно, уравнения вычитаем.

Имеем:

32q = -112

q = -3,5

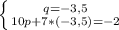
$\left \{ {{q = -3,5} \atop {10p + 7 * ( -3,5) = -2}} \right.$

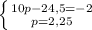
$\left \{ {{10p - 24,5 = -2} \atop {p = 2,25}} \right.$

Здесь делается все то же самое, что и в первой системе.

Весь основной материал я рассказал в начале.

Задача решена.

Понятно ли я объяснил задачи?

4,4(14 оценок)

Ответ:

EzNoobXex

22.01.2020

Составлю сначала формулу расчёта среднего арифметического:

(a + 4) / 2. Думаю, что по этой формуле вопросов не будет.

Составлю теперь формулу среднего геометрического или иначе среднего пропорционального этих чисел.

√4a = 2√a

и приравняю их, решим таким образом обычное иррациональное уравнение.

(a+4)/2 = 2√a

Я рекомендую решать уравнения такого типа путём последовательного возведения обеих его частей в квадрат, но прежде домножу обе части уравнения на 2, чтобы избавиться от знаменателя дроби в левой части.

a+4 = 4√a

Теперь выполню возведение обеих частей в квадрат.

(a+4)² = 16a

И далее имеем:

a² + 8a + 16 = 16a

a²- 8a + 16 = 0

По теореме Виета нахожу корни:

a1 = 4; a2 = 4

То есть, a = 4. При этом значении соблюдается вышеуказанное равенство.

4,6(64 оценок)

Это интересно:

01.04.2023