и 
. Чтобы найти для них общий знаменатель, нужно найти найменьшее общее число которое нацело делилось бы на знаменатель первого и второго дроба, в даном случае знаменатели это 25 и 4. Ну можно взять больший знаменатель умножить на 2 и проверить делится ли это число нацело на первый и другой знаменатель, если не делится ужножаеш на 3 и проверяеш, и так далее. Часто бывает, что один с знаменателей уже делится на себя и на второй знаменатель, тогда это и будет общий знаменатель. Потом оно само будет получаться, потому что будешь знать что на что делится.+ ;
;
= 
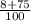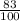, если можно сократить (то есть и числитель и множитель делится на одинаковое число), то сокращаем.
Для того чтобы найти промежутки возрастания и убывания необходимо взять производна от данной функции и решить следующие неравенстваy' (x) 0 при х удовлетворяющих этому неравенству функция возрастает Найдем y' (x) = (0.5cos (x) - 2) '=-0.5sin (x) Теперь решим неравенство:-0.5sin (x) 0 Это неравенство имеет решения при Значит на этих интервалах функция убывает. Теперь рассмотри неравенство - 0.5sin (x) >0 оно эквивалентно неравенству: sin (x) <0 И имеет следующие решения: Значит на этих интервалах функция возрастает. На границах интервалов функция имеет точку перегиба. ответ: Функция y=0,5cos (x) - 2 возрастает при Убывает при И имеет точки перегиба при