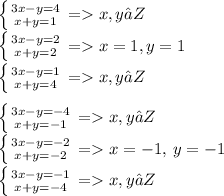
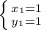

Двухзначное число больше удвоенного произведения его цифр на 5, а от удвоенной суммы цифр - на 3. Найдите эти число.
Решение.
Пусть x - цифра десятков данного числа;
y - цифра единиц этого числа
тогда
(10x+у) - данное двухзначное число.
ОДЗ: х∈N; 1≤x≤9;
y∈N; 0≤y≤9
По условию 10х+у > 2·(x·y) на 5.
Получаем первое уравнение:
10x+у - 2xy = 5
И ещё по условию 10х+у > 2·(x+y) на 3.
Получаем второе уравнение:
10x+у - 2·(x+y) = 3
Упростим его:
10x+у-2x-2y = 3
8х - у = 3
Решаем систему:
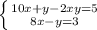
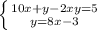
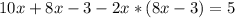
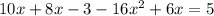
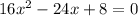
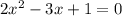
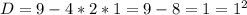
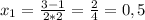 ∉N
∉N
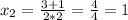
y=8x-3 при x=1
y=8·1-3
y=5
1- цифра десятков данного числа;
5 - цифра единиц этого числа
ответ: 15.
а) 9х+2у-4=0 9х+2у-4=0
8х+у-2=0 ⇒ второе умножаем на -2 ⇒ -16х-2у+4=0 складываем
⇒ -7х=0 , х=0, у=2
б) 5u+7v+3=0 -10u+14v+6=0
10u-v+6=0 ⇒ первое уравнение умножаем на -2 ⇒ 10u-v+6=0
⇒складываем ⇒ 13v=-12, v = - 12/13, u= 9/13
a) 4х-3у=8 , 8х-6у=9.
из первого выражаем х=(8+3у)/4, подставляем во второе
(8+3у)*8/4 -6у=9, ⇒решений нет!
б) 0,5х-у=0,5 , х-2у=1;
из первого выражаем у=0,5х-0,5
подставляем во второе
х-х+1=1
у,х∈R
(3x-y)(x+y)=4
1) (3x-y)(x+y)=4*1
3x-y=4
x+y=1
Суммируем эти уравнения:
4x=5
x=0,8 ∉.
Аналогично:
3x-y=1
x+y=4
x=0,8 ∉.
2) (3x-y)((x+y)=2*2
3x-y=2
x+y=2
Суммируем эти уравнения:
4x=4 |÷4
x₁=1 ⇒ y₁=2-1=1.
3) (3x-y)(x+y)=(-2)(-2)
3x-y=-2
x+y=-2
Суммируем эти уравнения:
4x=-4 |÷4
x₂=-1 ⇒ y₂=-2+1=-1
ответ: x₁=1 y₁=1 x₂=-1 y₂=-1.