Алгебра: Решите уравнение |x+1|-|x-2|+|3x+6|=5

Решите уравнение |x+1|-|x-2|+|3x+6|=5

👇

Увидеть ответ

Ответ:

013Angelina139

09.04.2023

X+1-x-2+3x+6=5
5x+5=5
5x=10
x=10:5
x=2

4,8(28 оценок)

Открыть все ответы

Ответ:

valu49

09.04.2023

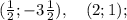
$(\frac{1}{2}; -3\frac{1}{2}), \quad (2; 1);$

Объяснение:

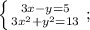
$\left \{ {{3x-y=5} \atop {3x^{2}+y^{2}=13}} \right. ;$

Выражаем из верхнего уравнения переменную "у":

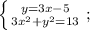
$\left \{ {{y=3x-5} \atop {3x^{2}+y^{2}=13}} \right. ;$

Подставляем полученное выражение в нижнее уравнение вместо "у":

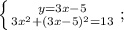
$\left \{ {{y=3x-5} \atop {3x^{2}+(3x-5)^{2}=13}} \right. ;$

Раскрываем квадрат разности двух выражений, пользуясь следующей формулой:

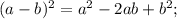
$(a-b)^{2}=a^{2}-2ab+b^{2};$

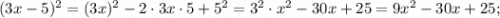
$(3x-5)^{2}=(3x)^{2}-2 \cdot 3x \cdot 5+5^{2}=3^{2} \cdot x^{2}-30x+25=9x^{2}-30x+25;$

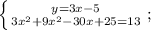
$\left \{ {{y=3x-5} \atop {3x^{2}+9x^{2}-30x+25=13}} \right. ;$

Приведём подобные слагаемые. Для этого вынесем общий множитель за скобки:

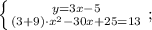
$\left \{ {{y=3x-5} \atop {(3+9) \cdot x^{2}-30x+25=13}} \right. ;$

Выполним сложение в скобке и перенесём слагаемое 13 со знаком минус в левую часть уравнения:

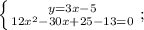
$\left \{ {{y=3x-5} \atop {12x^{2}-30x+25-13=0}} \right. ;$

Выполним вычитание:

$\left \{ {{y=3x-5} \atop {12x^{2}-30x+12=0}} \right. ;$

Разделив все части нижнего уравнения на 6, получим:

$\left \{ {{y=3x-5} \atop {2x^{2}-5x+2=0}} \right. ;$

Теперь разделим все части нижнего уравнения на 2 для того, чтобы получить приведённое квадратное уравнение:

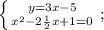
$\left \{ {{y=3x-5} \atop {x^{2}-2\frac{1}{2}x+1=0}} \right. ;$

Решаем нижнее уравнение по теореме Виета. Согласно ей, сумма корней приведённого квадратного уравнения равна коэффициенту при "х", взятому с противоположным знаком, а их произведение — свободному члену:

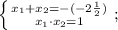
$\left \{ {{x_{1}+x_{2}=-(-2\frac{1}{2})} \atop {x_{1} \cdot x_{2}=1}} \right. ;$

Минус перед скобкой и минус после скобки дают плюс:

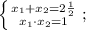
$\left \{ {{x_{1}+x_{2}=2\frac{1}{2}} \atop {x_{1} \cdot x_{2}=1}} \right. ;$

Корнями этой системы являются числа 1/2 и 2.

Мы нашли два значения переменной "х". Теперь подставим каждое из них в верхнее уравнение:

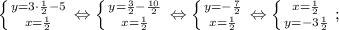
$\left \{ {{y=3 \cdot \frac{1}{2}-5} \atop {x=\frac{1}{2}}} \right. \Leftrightarrow \left \{ {{y=\frac{3}{2}-\frac{10}{2}} \atop {x=\frac{1}{2}}} \right. \Leftrightarrow \left \{ {{y=-\frac{7}{2}} \atop {x=\frac{1}{2}}} \right. \Leftrightarrow \left \{ {{x=\frac{1}{2}} \atop {y=-3\frac{1}{2}}} \right. ;$

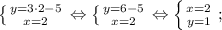
$\left \{ {{y=3 \cdot 2-5} \atop {x=2}} \right. \Leftrightarrow \left \{ {{y=6-5} \atop {x=2}} \right. \Leftrightarrow \left \{ {{x=2} \atop {y=1}} \right. ;$

Мы получили две пары корней:

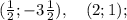
$(\frac{1}{2}; -3\frac{1}{2}), \quad (2; 1);$

Они являются решениями системы.

4,4(15 оценок)

Ответ:

пепоам

09.04.2023

1. Чтобы записать уравнение окружности, не хватает радиуса.

Стоит отметить, что расстояние от центра окружности до прямой x=3 равно радиусу, так как окружность касается этой прямой.

Центр имеет абсциссу, равную -1, а прямая -- равную 3

Найдём расстояние между -1 и 3:

R = |-1| + |3| = 1 + 3 = 4 -- радиус окружности

Теперь запишем уравнение окружности:

(x - x₀)² + (y - y₀)² = R², где (x₀, y₀) -- координаты центра окружности, R -- её радиус

(x + 1)² + (y - 5) = 16

2. Чтобы функция была чётная, нужно выполнение равенства:

y(x) = y(-x)

y(x) = xⁿ * xⁿ⁻² - 4

y(-x) = (-x)ⁿ * (-x)ⁿ⁻² - 4 = (-1 * x)ⁿ * (-1 * x)ⁿ⁻² - 4 = (-1)ⁿ * xⁿ * (-1)ⁿ⁻² * xⁿ⁻² - 4 = (-1)ⁿ⁺ⁿ⁻² * xⁿ * xⁿ⁻² - 4 = (-1)²⁽ⁿ⁻¹⁾ * xⁿ * xⁿ⁻² - 4 = 1ⁿ⁻¹ * xⁿ * xⁿ⁻² - 4 = xⁿ * xⁿ⁻² - 4

Итого y(x) = y(-x), следовательно функция чётная

3. Сначала отдельно рассмотрим первый корень. Рассмотрим подкоренное выражение, соберём из него квадрат суммы (a+b)² = a² + 2ab + b²:

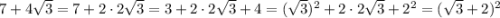
$7+4\sqrt{3}=7+2 \cdot 2\sqrt{3}=3+2 \cdot 2\sqrt{3}+4=(\sqrt{3} )^2+2 \cdot 2\sqrt{3} +2^2=(\sqrt{3}+2)^2$

Тогда выражение примет вид:

$\sqrt[10]{7+4\sqrt{3}} \cdot\sqrt[5]{\sqrt{3}-2}= \sqrt[10]{(\sqrt{3}+2)^2} \cdot\sqrt[5]{\sqrt{3}-2}= \sqrt[5]{\sqrt{3}+2} \cdot\sqrt[5]{\sqrt{3}-2}= \sqrt[5]{(\sqrt{3}+2)(\sqrt{3}-2)} =\sqrt[5]{(3-4)}=\sqrt[5]{-1}=-1$