и 
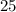– среднеарифметическое равно 
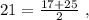и при этом 
на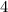 
меньше двадцати пяти и на 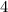больше семнадцати.
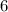монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на 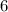монет меньше изначального, а у Пети на 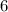монет больше изначального. А значит, вначале у Васи было на 
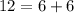монет больше, чем у Пети.
монет. Тогда у Пети 
монет.
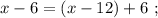
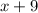монет, а у Пети-II будет 
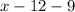монет. При этом у Пети-II монет в 
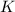раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в 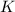раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение: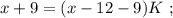
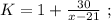
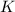было целым, целой должен быть и результат деления в дроби, а чтобы 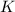было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда 
откуда: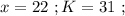
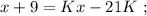
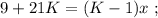
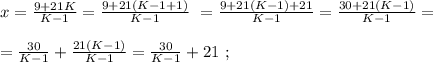
было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет 
откуда: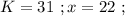
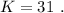
Объяснение:
Пусть дан квадратный трёхчлен x²+b*x+c. Если требуется выделить из этого выражения полный квадрат, то это означает, что это выражение нужно представить в виде (x+d)²+e, где d и e - неизвестные пока числа. Задача сводится к их нахождению. Раскрывая скобки, получаем выражение x²+2*d*x+d²+e, которое должно быть тождественно выражению x²+b*x+c. То есть должно выполняться тождество x²+2*d*x+d²+e≡x²+b*x+с. Это тождество будет иметь место в том случае, если будут выполнены равенства 2*d=b и d²+e=c. Поэтому для выделения полного квадрата нужно решить систему уравнений:
2*d=b
d²+e=c
Из первого уравнения находим d. Подставляя его затем во второе уравнение, находим e.
Примеры:
1) дан квадратный трёхчлен x²+4*x+8. В этом случае b=4 и c=8, поэтому система уравнений будет такова:
2*d=4
d²+e=8
Решая её, находим d=2 и e=4. Поэтому x²+4*x+8=(x+2)²+4.
2) дан квадратный трёхчлен x²-4*x+6. В этом случае b=-4 и c=6, поэтому система уравнений будет такова:
2*d=-4
d²+e=6
Решая её, находим d=-2 и e=2. Поэтому x²-4*x+6=(x-2)²+2.
Пусть теперь дан квадратный трёхчлен общего вида: a*x²+b*x+c, где a≠1. Так как a≠0, то разделив этот трёхчлен на a, получим выражение вида a*(x²+x*b/a+c/a). если теперь обозначить b/a=b1, c/a=c1, то это выражение запишется в виде a*(x²+b1*x+c1). Выделяя полный квадрат из трёхчлена x²+b1*x+c1, получим: a*x²+b*x+c=a*[(x+d)²+e], где d и e находятся из системы уравнений:
2*d=b1
d²+e=c1.
Примеры:
1. дан квадратный трёхчлен 3*x²+4*x+8. В этом случае a=3, b=4 и c=8. Разделив его на 3, получим выражение 3*(x²+4*x/3+8/3). Поэтому в данном случае b1=4/3, c1=8/3 и система уравнений для определения d и e будет такова:
2*d=4/3
d²+e=8/3
Решая её, находим d=2/3 и e=20/9. Поэтому 3*x²+4*x+8=3*[(x+2/3)²+20/9].
2. дан квадратный трёхчлен 3*x²-4*x+6. В этом случае a=3, b=-4 и c=6. Разделив его на 3, получим выражение 3*(x²-4*x/3+2). Поэтому в данном случае b1=-4/3, c1=2 и система уравнений для определения d и e будет такова:
2*d=-4/3
d²+e=2
Решая её, находим d=-2/3 и e=14/9. Поэтому 3*x²-4*x+6=3*[(x-2/3)²+14/9].