1. По условию a1=4, an+1 = -2•an + 4.
a2 = -2•a1 + 4 = - 2•4 + 4 = - 8 + 4 = -4.
a3 = -2•a2 + 4 = - 2•(-4) + 4 = 8 + 4 = 12.
ответ: 4; -4; 12.
2. По условию cn = 3 - 8n.
а) Если сn = 53, то
53 = 3 - 8n
8n = 3 - 53
8n = -50
n = - 50/8
n не является натуральным числом, поэтому 53 не является членом этой последовательности.
б) Если сn = 75, то
75 = 3 - 8n
8n = 3 - 75
8n = - 72
n = - 9
-9 не является натуральным числом, поэтому 75 не является членом этой последовательности.
ответ: оба числа не являются членами последовательности.
6
Объяснение:
Поскольку 0 /0 является неопределенностью, применим правило Лопиталя. Правило Лопиталя утверждает, что предел частного функций равен пределу частного их производных.
https://ru-static.z-dn.net/files/ddd/989db8841fa36ded4c6649b887486040.png
Найти производную числителя и знаменателя
https://ru-static.z-dn.net/files/da3/537abd52719773d58e2a66c9d6599372.png
Возьмем предел каждого члена.
https://ru-static.z-dn.net/files/da0/cb4a24132c2ef0dc9bf820799871b617.png
Определяем пределы, подставляя 3 вместо всех вхождений x .
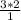
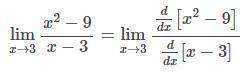
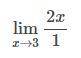
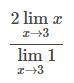
дробь не имеет смысла в том случае,если знаменатель равен 0. получаем: x*(x+7)=0, x=0 или x+7=0. x1=0, x2= -7. ответ: алгебраическая дробь не имеет смысла при при x=0 и (-7).