Графики функций не пересекают ось Х при У=0, поэтому:
1) x^2 + 1 = 0
x^2=-1 , следоват. =>
график функции не пересекает ось Х
2) x^2 -1=0
x=+-1 =>
график функции пересекает ось Х
3) -x^2+1=0
-x^2=-1
x^2=1
x=+-1 =>
график функции пересекает ось Х
4) -x^2-1=0
-x^2=1
x^2=-1 следоват. =>
график функции не пересекает ось Х
ответ: 1) ; 4)
ответ: n ∈ (-∞; -√12] ∪ [+√12; +∞).
x² + nx + 3n = 0,
Это совсем как квадратное уравнение, в котором нужно найти x. Выполним первый шаг, найдем дискриминант:
D = √(b² - 4ac) = √(n² - 4*1*3) = √(n² - 12).
Мы знаем, что из отрицательных чисел корень нельзя извлечь (в рамках действительных чисел), так что на дискриминант такое ограничение:
n² - 12 ≥ 0, то есть n² ≥ 12.
Решив это уравнение, получаем, что:
n ∈ (-∞; -√12] ∪ [+√12; +∞).
Это означает, что x - любое действительное число от минус бесконечности до -√12 включительно, а также от +√12 включительно до плюс бесконечности.
То есть n может быть равен, например, +√12, -√12, -100, - 45, 100 и так далее, но не может быть равен 0, 1, 5, -7, -11 и так далее.
=> 
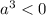т.е. первое утверждение неверно
=> 
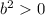
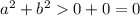
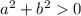
1)не пересекает оси напрвлены вверх, вершина параболы поднята над оью Х на 1
2)-пересекает ось х, парабола опущена на -1
3)- пересекает оси напрвлены вниз , а сама парабола поднята на 1
4) не пересекает