Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
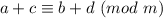
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
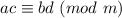
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
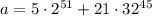
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,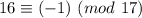 
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что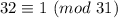 
, получаем
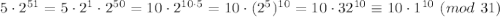
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
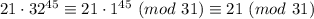
Остаток 21, чудесно. Выполняем последний шаг.
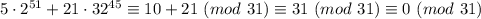
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
угол—геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
равные фигуры—Фигуры, которые совпадают при наложении называются РАВНЫМИ
середина отрезка—точка, которая делит данный отрезок на две равные части.
биссектриса угла—называется луч, который исходит из вершины и делит угол на две равные части (пополам). Биссектрисой угла называется луч, который исходит из вершины и делит угол на две равные части (пополам).
прямой угол—угол в радиан или 90°, половина развёрнутого угла. Угол, стороны которого перпендикулярны друг другу. При пересечении перпендикулярных прямых образуются прямые углы
тупой угол—Если градусная мера угла больше 90 и меньше 180 градусов, то такой угол называют тупым
острый угол—угол который больше 90 градусов!
смежные углы—это два угла, у которых одна сторона общая, а две другие являются дополнительными полупрямыми.Таким образом, вместе смежные углы составляют развёрнутый угол. Поэтому сумма величин смежных углов 180 градусов. То есть, величина угла, являющимся смежным для угла величиной α градусов, будет градусов.
вертикальные углы—пары углов с общей вершиной, образуемые при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
перпендикулярные прямые—
Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим взаимно перпендикулярным прямым, лежащим в одной плоскости. Две прямые, лежащие в одной плоскости, называются перпендикулярными, если они образуют четыре прямых угла
треугольник-Геометрическая фигура, образованная тремя пересекающимися прямыми, образующими три внутренних угла, а также всякий предмет, устройство такой формы.