1) Найти наибольшее значение функции
y = 1 - log₉ 3^(-x) на отрезке [-1; 5]
Преобразуем функцию
y = 1 - 0,5log₃ 3^(-x)
y = 1 + 0,5х·log₃ 3
y = 1 + 0,5х
находим производную:
y' = 0,5
Производна всегда больше нуля, следовательно, функция у возрастает.
Наибольшее значение находится на правом краю интервала [-1; 5], т.к при х = 5.
у наиб = у(5) = y = 1 + 0,5·5 = 3,5
2) Решить уравнение: 13^(5x-1) · 17^(2x-2) = 13^(3x+1).
17^(2x-2) = 13^(3x+1): 13^(5x-1)
17^(2x-2) = 13^(-2x+2)
17^(2x-2) = 1/13^(2x-2)
(17·13)^(2x-2) = 1
(17·13)^(2x-2) = (17·13)^0
2x - 2 = 0
2х = 2
х = 1
3) Вычислить значение выражения: 8^log8 6 + 625^log25 sqrt(13)
8^log₈ 6 + 625^log₂₅ √13 = 6 + 25^2log₂₅√13 = 6 + 25^log₂₅13 = 6 + 13 = 19
Необходимым условием сходимости ряда, но не достаточным, является стремление общего члена к нулю.
1) 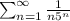
Как видим общий член при n -> ∞ стремится к нулю. Ряд у нас положительный, применим признак Даламбера (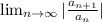 )
)
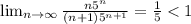
т.е. ряд сходится абсолютно
2) Ряд является знакочередующимся, применим признак Лейбница (Если члены знакочередующегося ряда убывают по модулю, то ряд сходится.)
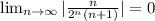
- ряд сходится. Исследуем также на абсолютную и условную сходимости (Сходящийся ∑a(n) называется сходящимся абсолютно, если сходится ряд из модулей ∑|a(n)|, иначе — сходящимся условно.)
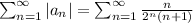
воспользуемся признаком сравнения
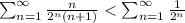
ряд справа сходится, т.е. наш ряд сходится абсолютно.
3) 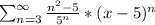
Воспользуемся признаком Даламбера
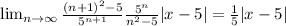
Наш ряд будет сходится, если ⅕|x-5|<1 ⇔ |x-5|<5 ⇔ -5<x-5<5 ⇔ 0<x<10
Остается исследовать сходимость на концах интервала:
a) x=0
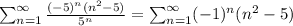
ряд расходится
б) x=10
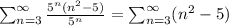
ряд расходится
Т.е. область сходимости ряда (0, 10)
400/100*40=160 уч. - обучается в 1 корпусе
160/2=80 уч - обучается в 3 корпусе
400-(80+160)=160 уч - обучается во 2 корпусе.
Утверждение верное, что в 1 и 2 корпусе обучается одинаковое количество обучающихся.