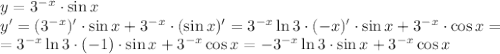
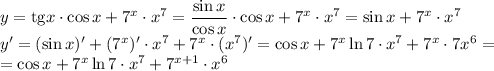
Для того чтобы представить квадратный трёхчлен х2-6х+9 в виде произведения нужно:
1. Решите соответствующее трёхчлену квадратное уравнение
2. Разложите на множители по формуле а*(х-х1)*(х-х2), где а-коэффициент перед х2, х-х, х1 и х2 - корни квадратного уравнения
3. Запишите ответ и при необходимости сделайте проверку
Решение
1. Решим квадратное уравнение х2-6х+9=0
х2-6х+9=0
а=1, в=-6, с=9
Д = в2-4*а*с = 36-4*9 = 0
т.к. Д=0 будет один корень
х= -в/2а = 6/2 = 3
2. а*(х-х1)*(х-х2)
Подставим
Получим: -6(х-3)(х-3)
Проверка
-6(х-3)(х-3) = (-6х+18)(х-3) = -6х2+18х+18х-54 = -6х2+36х-54
Разделим на -6; Получим: х2-6х+9 - первоначальный трёхчлен, из этого следует, что заданый трёхчлен верно разложен на множители.
ответ: -6(х-3)(х-3)
1) a) 4+12x+9x2
4+12x+18
22+12x
2(11+6x)
б) 25-40х+16х2
25-40х+32
57-40х
г) -56а+49а*2+16
-56а+98а+16
42а+16
2(21а+8)
2) a) (y-1)(y+1) б) p^2-9 г) (3x-2)(3x+2) д) (3x)^2-2^2 е) a^2-3^2
y^2-1 (3x)^2-2^2 9x^2-4 a^2-9
в) 4^2-(5y^2) 9x^2-4
16-25y^2
4) a) a3-b3 б) 27a3+8b3
3(a-b) 81a+24b
3(27a+8b)