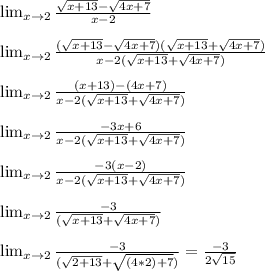Алгебра: Решите по вынести множитель из под знака

Решите по вынести множитель из под знака

👇

Ответ:

IVIOPGAN

17.07.2020

Все мы родом из детства — веселого, озорного, счастливого и безвозвратного. каждый из нас частенько окунается в детские воспоминания, неважно веселые или грустные, зато всегда неповторимые. дети по своей природе бесхитростны и открыты. они стремительно растут и познают чудесный окружающий мир. даже сталкиваясь с первыми неудачами, дети не особенно расстраиваются и не принимают близко к сердцу многие неприятные моменты. к сожалению, с возрастом мы утрачиваем эту детскую наивность и становимся слишком уязвимыми или, даже, предвзятыми. повезло тому, кто сумел сохранить непосредственность ребенка в своем сердце, хоть немного смягчив его прагматизм. дети часто смеются и радуются без особой на то причины, и это замечательно. получать положительные эмоции из любой, незначительной мелочи – это талант каждого ребенка, который, увы, впоследствии теряется в суете житейских передряг. поэтому, вспоминая о детстве, наши лица просветляются, а глаза оживают и загораются озорными огоньками. мы расслабляемся и раскрываемся навстречу друг другу. и будет здорово, если мы, как можно дольше, сможем оставаться детьми.

4,6(27 оценок)

Открыть все ответы

Ответ:

vovakornev2002

17.07.2020

Левая часть неравенства должна существовать, поэтому
a + x >= 0,
a - x >= 0

Переписываем систему в виде
-a <= x <= a,
|x| <= a
откуда видно, что a >= 0.
Можно сразу записать, что если a < 0, то решений нет.

Тогда обе части исходного неравенства неотрицательные, и можно возводить в квадрат.
a + x + 2sqrt(a^2 - x^2) + a - x > a^2
sqrt(a^2 - x^2) > a(a - 2)/2

Если правая часть отрицательна, то решение неравенства - все значения, при которых корень существует.
a(a - 2)/2 < 0 при 0 < a < 2, так что еще одна часть ответа такова: если 0 < a < 2, то -a <= x <= a.

Осталось рассмотреть случай, когда a(a - 2) >= 0. Тогда вновь можно возводить неравенство в квадрат.
a^2 - x^2 > (a^4 - 4a^3 + 4a^2)/4
x^2 < a^3 (4 - a)/4.

У этого неравенства есть шанс иметь решения, если правая часть строго положительна, поэтому предпоследняя часть ответа: если a = 0 или a >= 4, решений нет. Осталось рассмотреть последний случай 2 <= a < 4.

Заметим, что при таких a правая часть меньше a^2, ведь
a^3 (4 - a) / 4 / a^2 = a (4 - a) / 4 < 2 * (4 - 2) / 4 = 1 (известно, что квадратичная парабола a (4 - a) / 4 достигает максимального значения в вершине), поэтому все корни существуют, и последняя часть ответа: если 2 <= a < 4, то -sqrt(a^3 (4 - a))/2 < x < sqrt(a^3 (4 - a))/2.

Собираем всё в одно и получаем ответ.
ответ. Если 0 < a < 2, то -a <= x <= a; если 2 <= a < 4, то -sqrt(a^3 (4 - a))/2 < x < sqrt(a^3 (4 - a))/2, для остальных a решений нет.

4,8(64 оценок)

Ответ:

лия206

17.07.2020

Главное избавиться от корней в разности корней, для этого функцию и умножают на выражение, сопряжённое разности корней.

Сопряжённое выражение - это то же выражение, но с противоположным знаком.

Умножим и числитель, и знаменатель на СУММУ тех же корней. В итоге в числителе получится разность квадратов, и корни в числителе сгорят.

Бояться этой суммы корней в знаменателе не стоит, просто продолжим упрощать выражение насколько возможно, а затем просто подставим число, к которому стремится предел. И получится ответ, идеально подходящий к имеющемуся у вас шаблону.

$\lim_{x \to 2} \frac{\sqrt{x+13}-\sqrt{4x+7}}{x-2}\\\\\lim_{x \to 2} \frac{(\sqrt{x+13}-\sqrt{4x+7})(\sqrt{x+13}+\sqrt{4x+7})}{x-2(\sqrt{x+13}+\sqrt{4x+7})}\\\\\lim_{x \to 2} \frac{(x+13)-(4x+7)}{x-2(\sqrt{x+13}+\sqrt{4x+7})}\\\\\lim_{x \to 2} \frac{-3x+6}{x-2(\sqrt{x+13}+\sqrt{4x+7})}\\\\\lim_{x \to 2} \frac{-3(x-2)}{x-2(\sqrt{x+13}+\sqrt{4x+7})}\\\\\lim_{x \to 2} \frac{-3}{(\sqrt{x+13}+\sqrt{4x+7})}\\\\\lim_{x \to 2} \frac{-3}{(\sqrt{2+13}+\sqrt{(4*2)+7})}=\frac{-3}{2\sqrt{15}}$