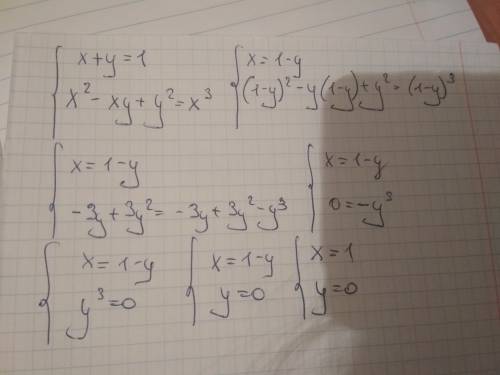
прощения, что не в рукописном варианте, но думаю, что ход мыслей будет понятен=)
Нужно помнить, про то, что значение x, стоящего под логарифмом - всегда строго больше нуля (ОДЗ: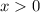 
).
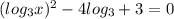
Пусть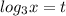 
, тогда:
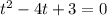
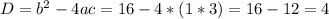
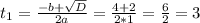
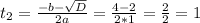
Тогда:
1). 
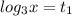
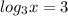(теперь нужно представить 3 так, чтобы под логарифмом было такое число, которое с основанием логарифма 
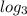будет равняться 3 (иначе говоря 3 в степени 3 (первая 3 - для того, чтобы сократить 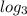и после этого осталась чистая степень - 3)
(таким числом под логарифмом будет 27: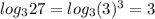 
)
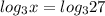(одинаковые логарифмы с основанием 3>1 - можем их убрать)
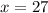
2). 
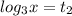
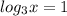(сделаем тоже самое: нужно представить 1 так, чтобы под логарифмом было такое число, которое с основанием логарифма 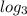будет равняться 1 (иначе говоря 3 в степени 1 (3 - для того, чтобы сократить 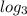и после этого осталась чистая степень - 1))
(таким числом под логарифмом будет 3: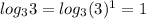 
)
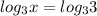(одинаковые логарифмы с основанием 3>1 - можем их убрать)
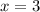
ответ: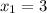 
, 
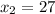
Объяснение:
Мы знаем, что помимо положительных чисел, меньше нуля существуют еще и отрицательные числа.
Поэтому, при сложении отрицательного и положительного числа, всегда из положительного числа вычитается отрицательное, то есть, наглядно первый пример можно преобразовать как:
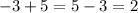, тогда становится понятнее логика сложения отрицательного с положительным числом.
Второй пример аналогичен первому: если из положительного числа, то есть 3, вычесть отрицательное число, то есть 5, получим как раз -2: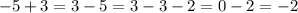 
.
Пойдем ниже, в третьем примере из положительного числа вычитают большее отрицательное число. Поэтому в таких случаях запись можно преобразовать как: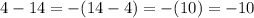 
, то есть, мы из отрицательного числа вычитаем положительное число и заносим эту операцию над двумя числами в скобки со знаком "минус".
Четвертый и пятый пример аналогичны первому, когда мы можем представить запись в виде:
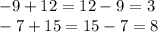
То есть, если число со знаком "+" больше числа со знаком "-", мы имеем право переписать запись в виде обычного вычитания из большего числа меньшее, где получим положительное число в ответе.
