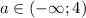Question

Найдите все значения параметра а, при каждом из которых ур-е имеет 1 решение: x^3-x+2=-x^2+ax-1

Answer 1

$x^3-x+2=-x^2+ax-1\Leftrightarrow ax=x^3+x^2-x+3$

Так как x = 0 не является корнем уравнения, поделим обе части на x.

$a=x^2+x-1+\frac{3}{x}$

Обозначим правую часть как f(x). Найдём производную этой функции:

$f'(x)=2x+1-\frac{3}{x^2}=\frac{2x^3+x^2-3}{x^2}$

Заметим, что при x = 1 числитель равен нулю. Разложим его на множители: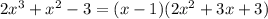 $2x^3+x^2-3=(x-1)(2x^2+3x+3)$. Второй множитель разложить нельзя, так как, приравняв его к нулю, мы не сможем найти корни, ибо D < 0. Найдём знаки производной (см. фото 1). Зная это, можем прикинуть график функции (см. фото 2). Точка локального минимума - x = 1. f(1) = 4.

a = k (k - какое-то число) - прямая, параллельная оси Ox. По графику видно, что при a < 4 имеется ровно одно пересечение, то есть один корень.

ответ: $a\in(-\infty; 4)$