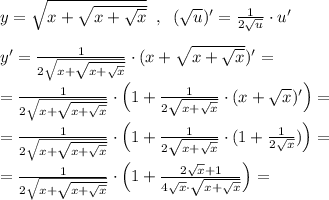
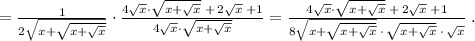
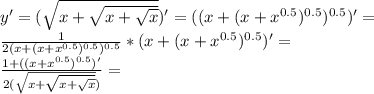
=>
=>
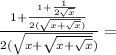
Дальше уже обыкновенные дроби, производных нет, привести к общему знаменателю, сократить и т.д.

=>
=>
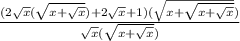
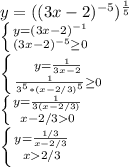
Первоначальная функция имеет следующею область определения: 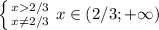
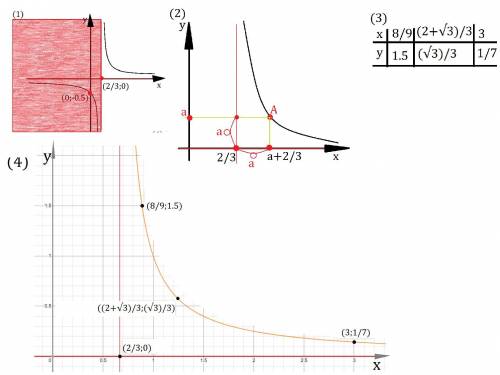
Построим схематично преобразованную функцию Y и наложим ограничение. График функции Y это гипербола, которая лежит в 1 и 3 четвертях относительно следующих прямых: y=0; x=2/3, которые так же являются асимптотами. Пересечение с осями координат: 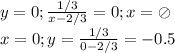
См. вниз. (1)
Что бы понять как именно убывает функция найдём не сколько точек.
У получившейся кривой есть точка, которая равноудалена от двух асимптот точка A. См. вниз (2)
Найдём координаты этой точки и ещё пару точек кривой, чтобы понять как быстро функция убывает.
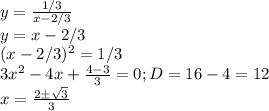
Существует только x>2/3.
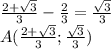
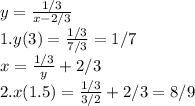
Для ясности нарисую табличку.
См. вниз (3)
Теперь строим график нашей функции.
См. вниз (4)