3)1;-3;9;-27 ,т.к.q=-3:1=-3 значит b3=-3*-3=9;b4=9*-3=-27
1. Укажите линейное уравнение с двумя переменными.
1) 3·x-5=0 - только одна переменная х
2) х/7-у/5=8/3 - линейное, переменные х и у
3) 7/х+5/у=3/8 - нелинейное
4) 7·x²+5·у=3 - уравнение 2-степени
2. Укажите уравнение, решением которого является пара чисел (1 3/7; 2 5/6) .
Проверим подставкой в уравнение:
1) 14·x-12·y+14=0
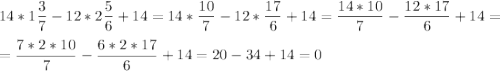
является решением, поэтому остальные уравнение не нужно проверить
2) 14·x-6·y-10=0
3) 10·x/7+17·y/6=27
4) x-6·y=17
3. Какая пара чисел является решением уравнения 3·x-2·y+5=0
1) (-1/3; -2) 2) (-2; -1/3) 3) (-4/3; -1/2) 4) (-3; 2)
Проверим подставкой в уравнение:

не является решением
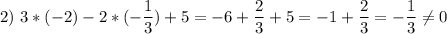
не является решением
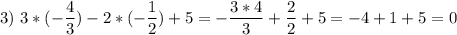
является решением, поэтому последнюю пару не нужно проверить
4. Какая из пар чисел является решением уравнением 2·x-y=6
1) (2; -1) 2) (5; 3) 3) (1; -4) 4) (-1; -3)
Проверим подставкой в уравнение:
1) 2·2-(-1)=4+1=5≠6 - не является решением
2) 2·5-3=10-3=7≠6 - не является решением
3) 2·1-(-4)=2+4=6=6 - является решением, поэтому последнюю пару не нужно проверить
Последовательности заданы несколькими первыми членами. Одна из них - геометрическая прогрессия. Найдите ее. И дайте решение.
1)1;3;5;7 2)1;-3;5;-7 3)1;-3;9;-27 4)1;-3;3;-1/3
Решение
Геометрическая прогрессия п3
где:
1-й член прогресии: b1=1
постоянный множитель (знаменатель прогрессии): q=-3
bn=b1*q^(n-1)
b2=1*(-3)^(2-1)=1*(-3)^1=-3
b3=1*(-3)^(3-1)=1*(-3)^2=9
b4=1*(-3)^(24-1)=1*(-3)^3=-27