Объяснение:
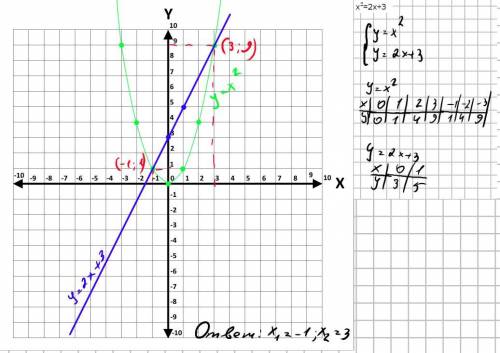
Для того чтобы решить уравнение вида x²=kx+m нам нужно по отдельности изобразить графики функции на системе координат (как показано на скриншоте ниже), и конечно же составить систему уравнений (так как мы ищем пересечение этих двух функций). То есть мы должны изобразить на графике 2 функции по отдельности это y=x² (парабола) и y=kx+m (прямая). В нашем случае x²=2x+3 мы должны изобразить параболу (y=x²) и прямую (2x+3), а для того чтобы их изобразить, мы просто составляем таблицу (как показано на скриншоте) и берем ЛЮБЫЕ значения X подставляем их в функцию и получаем Y например: Y=2X+3 берем любой X, для удобства возьмем 0, и подставим вместо X цифру 0 и получим Y=2*0+3=3, то есть при x=0 значение функции равно 3 то есть мы получили координаты некоторой точки на графике это (0;3) (сначала пишу X потом через точку с запятой пишут Y) и по этим координатам отмечаем эту точку, и так дальше продолжаем вычислять Y при разных X и в итоге получим график функции (для прямой достаточно найти 2 значения).
Я в тебя верю, станешь пилотом!
А вот я для тебя решил
А) Тянем первый билет, с вероятностью 3/15 = 1/5 мы вытянем выигрышный билет. Значит, осталось 14 билетов, среди которых уже 2 выигрышных билета. Тянем второй раз, вероятность вытянуть выигрышный билет равна 2/14 = 1/7. Следовательно, вероятность два раза подряд вытащить выигрыш равна 1/5 * 1/7 = 1/35.
б) Здесь надо рассмотреть два случая.
В первый раз вытаскиваем выигрыш (вероятность 3/15=1/5), во второй раз - нет (вероятность 12/14=6/7). Вероятность такой ситуации 1/5 * 6/7 = 6/35.
И другой случай, сперва вытаскиваем билет без выигрыша (вероятность 12/15=4/5), а во второй раз с выигрышем (вероятность 3/14). Вероятность этой ситуации 4/5 * 3/14 = 12/70 = 6/35
Суммируем вероятности обоих случаев 6/35 + 6/35 = 12/35
в) В первый раз не вытянули билет с выигрышем (вероятность 12/15=4/5) и во второй раз (вероятность 11/14). Итоговая вероятность такого варианта развития событий - 4/5 * 11/14 = 22/35