Question

√(n+√(n+√(n+√=m , где m и n неотрицательные, рациональные, целые числа, а корней 2019. найдите все возможные m и n, не обязательно различные. p.s. про 0 я знаю, по сути нужно доказать почему только 0 подходит

Answer 1

Итак, окончательно мы решили, что n и m - целые числа. Проделаем 2018 операций следующего вида: возводим равенство в квадрат и переносим n вправо. Получаем равенство

$\sqrt{n}=(\ldots((m^2-n)^2-n)^2-\ldots )^2-n$

Справа стоит целое число, n является его квадратом. Для нас важно только, что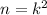 $n=k^2$ для некоторого целого неотрицательного числа.  Перенося n налево и заменяя 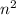$n^2$ на k, получаем равенство вида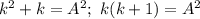 $k^2+k=A^2;\ k(k+1)=A^2$

1-й случай. k=0; n=0; m=0. Автор задачи про этот случай знает.

2-й случай. k>0. Докажем, что произведение двух соседних натуральных чисел не может быть полным квадратом. k=1; k+1=2, произведение равно 2 - это не есть полный квадрат. k=2; k+1=3; произведение равно 6 - это не есть полный квадрат. Почему ни при каком натуральном k произведение не может быть полным квадратом? Дело в том, что у соседних натуральных чисел не может быть общих множителей, кроме 1. Поэтому, если их произведение является полным квадратом, каждое из этих чисел должно быть полным квадратом, чего быть не может быть - единственный случай, когда расстояние между квадратами целых неотрицательных чисел равно 1 - это 0 и 1, а этот случай мы уже рассмотрели.

ответ: n=m=0