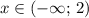у = kx + b
так как график проходит через начало координат, b = 0.
подставим координаты точки М в уравнение
4 = k * (-2.5)
Отсюда найдем k = 4/(-2.5) = -1.6
то есть искомая формула линейной функции у = -1,6х
Теперь, чтоб найти точку пересечения этого графика с прямой 3х-2у - 16 = 0, решим систему из 2 линейных уравнений
у = -1,6х
3х-2у - 16 = 0
подставив у из первого уравнения во второе, получим
3х + 3,2х - 16 = 0
6,2х = 16
х = 16/6,2= 80/31
тогда у = -1,6 *80/31 = -128/31
То есть искомая точка пересечения (80/31; -128/31)
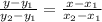

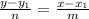
Заметим, что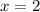 - единственный корень уравнения
- единственный корень уравнения 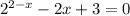 , следовательно, график функции
, следовательно, график функции 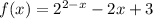 пересечёт ось абсцисс один раз в точке
пересечёт ось абсцисс один раз в точке 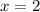 . С корнем и по непрерывности данной функции, поймём, где она будет отрицательна, а где - положительна. Для этого найдём значения функции в точках больше и меньше
. С корнем и по непрерывности данной функции, поймём, где она будет отрицательна, а где - положительна. Для этого найдём значения функции в точках больше и меньше 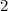 .
.
Значит, наша функция следовала из своих положительных значений и точку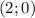 к отрицательным. Следовательно, функция была положительна при
к отрицательным. Следовательно, функция была положительна при 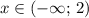 .
.
ответ.