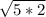Объяснение:
Пусть имеется некоторый реальный эксперимент и пусть через {\displaystyle {A}}{A} обозначен наблюдаемый в рамках этого эксперимента результат. Пусть произведено {\displaystyle n}n экспериментов, в которых результат {\displaystyle {A}}{A} может реализоваться или нет. И пусть {\displaystyle k}k — это число реализаций наблюдаемого результата {\displaystyle {A}}{A} в {\displaystyle n}n произведённых испытаниях, считая что произведённые испытания являются независимыми.
Числовая функция: {\displaystyle \mathrm {N} _{n}(k)={\frac {k}{n}}\Leftrightarrow {\frac {k(A,n)}{n}}}\mathrm{N} _{n}(k)={\frac {k}{n}}\Leftrightarrow {\frac {k(A,n)}{n}} называется функцией относительной частоты реализаций наблюдаемого результата {\displaystyle {A}}{A} в {\displaystyle n}n независимых реальных экспериментах. Вероятность вычисляют до опыта, а относительную частоту - после опыта.
Надо снести всё под единный корень и разложить на множители
теперь на множители
360/2 6,4/2
180/2 3,2/2
90/2 1,6/2
45/3 0,8/2
15/3 0,4/2
5 0,2/2
теперь выносим корни
2*3*2*2*2