Исследовать функцию f (x) = 12x/(9+x²) и построить ее график.
1. Область определения функции - вся числовая ось, так как знаменатель не может быть равен нулю.
2. Функция f (x) = 12x/(9+x²) непрерывна на всей области определения. Точек разрыва нет.
3. Четность, нечетность, периодичность:
f(–x) = 12*(–x)/(9+(–x)²) = –(12x(9+x²)) = –f(x).
Функция является нечетной. График функции симметричен относительно начала координат.
Функция непериодическая.
4. Точки пересечения с осями координат:
Ox: y=0, 12x/(9+x²) = 0 ⇒ x=0. Значит (0;0) - точка пересечения с осью Ox.
Oy: x = 0 ⇒ y = 0. Значит (0;0) - точка пересечения с осью Oy.
5. Промежутки монотонности и точки экстремума:
Находим производную заданной функции.x = 3, x = -3 критические точки.
Интервалы возрастания и убывания функции:6. Найдем точки перегибов, для этого надо решить уравнение
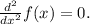
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
Вторая производная 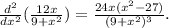
Приравниваем нулю и решаем это уравнение.
Для дроби достаточно нулю приравнять числитель:
24x(x²-27) = 0.
Решаем это уравнение: х = 0, х² - 27 = 0
Корни этого уравнения: х₁ = 0. х₂ = √27 =3√3, х₃ = -√27 = -3√3.
7. Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках
Выпуклая на промежутках
8. Искомый график функции дан в приложении.
-20,7≠-26,3 ⇒ A∉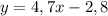
ответ: график не проходит через точку A