Данное двойное неравенство равносильно системе двух квадратных неравенств:
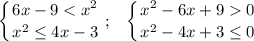
Первое неравенство  .
.
Заметим, что в левой части скрывается квадрат разности (формула  ):
): 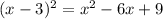 .
.
Неравенство принимает следующий вид: 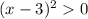 .
.
Так как квадрат числа всегда неотрицательный, то нам не подходит всего лишь один случай: 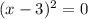 и
и 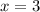 .
.
Значит, первой неравенство эквивалентно тому, что 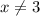 .
.
Второе неравенство 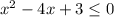 .
.
Вс уравнение 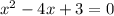 имеет по теореме Виета (утверждающей, что
имеет по теореме Виета (утверждающей, что 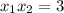 и
и 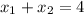 ) корни
) корни 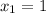 и
и 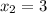 .
.
Из этого следует разложение левой части на множители: 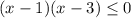 .
.
Метод интервалов подсказывает решение ![x \in [ 1; 3 ]](/tpl/images/1227/3957/60bcc.png) .
.
+ + + - - - + + +
_________![[ \; 1 \; ]](/tpl/images/1227/3957/d73a9.png) _________
_________![[ \; 3 \; ]](/tpl/images/1227/3957/abab5.png) _________
_________
\\\\\\\\\\\\\\\\\\\\\
Значит, второе неравенство равносильно тому, что  .
.
Имеем значительно более простую систему неравенств:

Вполне понятно, что ее решением является 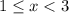 (как пересечения двух промежутков).
(как пересечения двух промежутков).
Или же 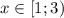 .
.
Задача решена!
ответ: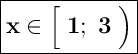
Для решения задачи необходимо определить производительность работы каждой из труб.
Представим весь объем воды в бассейне в виде 100% или 1.
В таком случае, за 1 час работы первая труба наполнит:
1 / 10 = 1/10 часть бассейна.
Вторая труба наполнит:
1 / 8 = 1/8 часть бассейна.
Находим продуктивность работы двух труб при совместной работе.
Для этого суммируем продуктивность каждой трубы.
1/10 + 1/8 = (Общий знаменатель 40) = 4/40 + 5/40 = 9/40.
В таком случае, после 1 часа совместной работы останется наполнить:
1 - 9/40 = 31/40 часть бассейна.
1=2/3+6х
1-2/3=6х
1/3=6х
х=1/3:6
х=1/18
=2/3+6ху
-2/3=2/3+6х
-2/3-2/3=6х
-1 1/3=6х
х=-1 1/3:6
х=-2/9
у=2/3+6х
5=2/3+6х
5-2/3=6х
4 1/3=6х
х=4 1/3:6
х=13/18
(второй на смогла , сорян ._.)