Question

Прогрессия из 4 натуральных членов имеет сумму 80. найдите её наибольший член.

Answer 1

Геометрическая прогрессия:

$b_1; \ b_1q; \ b_1q^2; \ b_1q^3$

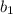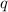По условию все члены - натуральные числа, значит $b_1$ и $q$ - натуральные

Найдем сумму первых 4 членов по формуле:

$S_n=\dfrac{b_1(q^n-1)}{q-1} \\\\S_4=\dfrac{b_1(q^4-1)}{q-1}=\dfrac{b_1(q-1)(q^3+q^2+q+1)}{q-1}=b_1(q^3+q^2+q+1)$

По условию эта сумма равна 80:

$b_1(q^3+q^2+q+1)=80$

Преобразуем левую часть:

$b_1(q+1)(q^2+1)=80$

Предположим, что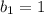 $b_1=1$. Тогда:

$(q+1)(q^2+1)=80$

Рассмотрим в качестве второго сомножителя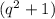 $(q^2+1)$ числа - делители числа 80.

$q^2+1=\{1;\ 2;\ 4;\ 5;\ 8;\ 10;\ 16;\ 20;\ 40;\ 80\}\\q^2=\{0;\ 1;\ 3;\ 4;\ 7;\ 9;\ 15;\ 19;\ 39;\ 79\}$

Имеется всего четыре точных квадрата:

$q^2=0\Rightarrow q=0$ - не геометрическая прогрессия.

$q^2=1\Rightarrow q=1$ (отрицательные значения не рассматриваем) - все члены прогрессии равны 1, их сумма равна 4 - не подходит.

$q^2=4\Rightarrow q=2$ - члены прогрессии равны 1, 2, 4, 8 в сумме дают 15 - не подходит.

$q^2=9\Rightarrow q=3$ - члены прогрессии равны 1, 3, 9, 27 в сумме дают 40 - не подходит.

При рассмотрении других значений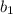 $b_1$, состав делителей числа 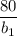$\dfrac{80}{b_1}$ будет уменьшаться, однако никаких новых чисел, отличных от ранее выписанных не будет.

Таким образом, остается определить может ли при каком-либо значении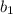 $b_1$ знаменатель равняться 1, 2 и 3.

Если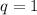 $q=1$, то последовательность постоянная. Очевидно. что каждый член такой прогрессии (если такие прогрессии допускаются по условию) равен 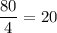$\dfrac{80}{4} =20$. Наибольший член в таком случае равен 20.

Если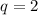 $q=2$, то рассмотрим формулу для суммы:

$\dfrac{b_1\cdot(2^4-1)}{2-1}=80\Rightarrow 15b_1=80\Rightarrow b_1=\dfrac{16}{3}$

16/3 - не натуральное число, такой случай не удовлетворяет условию

Если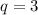 $q=3$, то также рассмотрим формулу для суммы:

$\dfrac{b_1\cdot(3^4-1)}{3-1}=80\Rightarrow 80b_1=160\Rightarrow b_1=2$

Следовательно, члены прогрессии 2, 6, 18, 54. Наибольший - 54.

Прогрессия 20, 20, 20, 20 с максимальным элементом 20 (если учитывать рассмотрение постоянных прогрессий со знаменателем 1, потому что слово "наибольший", возможно, предполагает то, что все члены последовательности должны быть различны).

Прогрессия 2, 6, 18, 54 с максимальным элементом 54.