Есть два метода решения данного уравнения: методом подстановки и методом исключения неизвестных.Я покажу их обоих.
ПодстановкаРешаем уравнение относительно x:
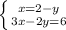
Поставить данное значение x в уравнение 3x-2y=6:
3(2-y)-2y=6
Решаем уравнение относительно y:
6-3y-2y=6
-3y-2y=0
-5y=0
y=0
Подставить данное значение y в уравнение x=2-y:
x=2-0
Решаем уравнение относительно x:
x=2
Решением системы является упорядоченная пара чисел (x,y):
(x,y)=(2,0)
Проверка:
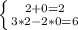
Упростить уравнения:

Упорядоченная пара числе является решением системы уравнений, т.к оба равенства верны:
(x,y)=(2,0)
ИсключениеУмножить обе части уравнения на -3:

Сложить уравнения для исключения по меньшей мере одной неизвестной:
-5y=0
Разделить обе стороны уравнения на -5:
y=0
Подставить данное значение y в простейшее уравнение x+y=2:
x+0=2
Решаем уравнение относительно x:
x=2
Дальше как в предыдущем примере
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная. Вертикальных асимптот - нет
2. Пересечение с осью Х. Решаем квадратное уравнение: Y=0
при х1,2 = - 1/3.
3. Пересечение с осью У. У(0) = 1.
4. Поведение на бесконечности.limY(-∞) = + ∞ limY(+∞) = +∞ - горизонтальных асимптот - нет.
5. Исследование на чётность.Y(-x) = 9*x² - 6*x+1 ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 18*x -6 = 0.
Корень Х= -1/3.
7. Локальные экстремумы. Минимум – Ymin(- 1/3) =0.
8. Интервалы возрастания и убывания. Возрастает - Х∈(-1/3;+∞),
убывает = Х∈(-∞;-1/3)
8. Вторая производная - Y"(x) = 18.
Корня производной - точка перегиба - нет.
9. Вогнутая – «ложка» Х∈(-∞;+∞).
10. Область значений Е(у) У∈(0;+∞)
11. Наклонная асимптота -. Уравнение: lim(oo)(k*x+b – f(x).
k=lim(∞)(9x+6+1)= ∞ - наклонных асимптот - нет
12. График в приложении.
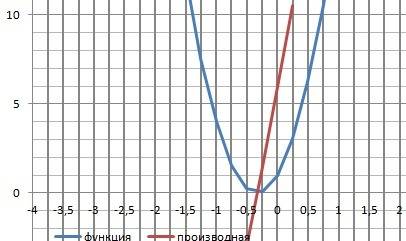
Решение системы приведено на фото