Question

Решить уравнение |x^2+9x+25|=5 с обьяснением

Answer 1

Вспомним правило работы с модулем: если внутри число неотрицательное, то подмодульное выражение раскрывается со своим знаком. Если же оно меньше нуля, то выражение выходит с противоположным знаком. Отсюда можем извлечь, что |5| = 5 и |-5| = 5. Тогда подмодульное выражение равно либо 5, либо -5. Решим эти два уравнения:

1) $x^2+9x+25=5\\x^2+9x+20=0$

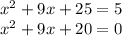
По теореме Виета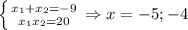 $\left \{ {{x_{1}+x_{2}=-9} \atop {x_{1}x_{2}=20}} \right. \Rightarrow x=-5;-4$

2) $x^2+9x+25=-5\\x^2+9x+30=0\\D=9^2-4*1*30=81-120$

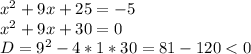
Здесь корней нет.

ответ: -5; -4

Answer 2

|x² + 9x + 25| = 5

или  x² + 9x + 25 = 5     или  x² + 9x + 25 = - 5

1) x² + 9x + 25 = 5

x² + 9x + 25 - 5 = 0

x² + 9x + 20 = 0

По теореме Виета :

x₁ = - 5        x₂ = - 4

2) x² + 9x + 25 = - 5

x² + 9x + 25 + 5 = 0

x² + 9x + 30 = 0

D = 9² - 4 * 30 = 81 - 120 = - 39 < 0

решений нет

ответ : - 5 ; - 4