Обозначим суточную норму потребления сена для лошади - х, для коровы - у. Две лошади - 2х, две коровы - 2у. Одна лошадь и две коровы - х+2у потребляют 34 кг.
Две лошади и одна корова - 2х+у - 35 кг.
Составим систему уравнений с двумя неизвестными:
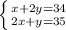
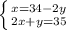
68 - 4y + y = 35
3y = 33
y = 11
x = 34 - 22 = 12
ответ: для одной лошади 12 кг сена, для одной коровы - 11 кг
В общем виде решение линейного неравенства с одной переменной
можно изобразить так:
1) Неизвестные переносим в одну сторону, известные — в другую с противоположными знаками:
2) Если число перед иксом не равно нулю (a-c≠0), обе части неравенства делим на a-c.
Если a-c>0, знак неравенства не изменяется:
Если a-c<0, знак неравенства изменяется на противоположный:
Если a-c=0, то это — частный случай. Частные случаи решения линейных неравенств рассмотрим отдельно.
Примеры.
Это — линейное неравенство. Переносим неизвестные в одну сторону, известные — в другую с противоположными знаками:
Обе части неравенства делим на число, стоящее перед иксом. Так как -2<0, знак неравенства изменяется на противоположный:
Так как неравенство строгое, 10 на числовой прямой отмечаем выколотой точкой. Штриховка от 10 влево, на минус бесконечность.
Так как неравенство строгое и точка выколотая, 10 записываем в ответ с круглой скобкой.
х кг сена - для 1лошади
у кг сена - для 1 коровы
х + 2у = 34
+ 2х + у = 35
3х + 3у = 69 / 3
х + у = 23
х = 23-у
23 - у + 2у = 34
у = 11 (кг) - сена для 1 коровы
(35 - 11) : 2 = 12(кг) - сена для 1 лошади