а и а^2 здесь можно представить в виде любого числа. Попробуем это сделать. Для начала, выясним, при каких значениях а=а^2. Естественно, условие выполняется при значении 0, также ему удовлетворяют значения 1 и -1. Возаедём их для ясности в квадрат и получим:
1×1=1
-1×(-1)=1. Следовательно, 1=1 и а =а^2.
Теперь выясним, почему же при других значениях а<а^2. Подставим нппример значение 2. Тогда получим, что 2^2=4 и 2<4. А если вдруг число будет отрицательным? Попробуем подставить и получим:
-2^2=-2×(-2)=4. Соответственно, получим такое неравенство:
2<-4. Проведя такое доказательство, можно прийти к выводу, что а<=а^2.
Найдите корни уравнения:
1) 7+2x²=2(x+1)(x+3)
постепенно раскрываем скобки
7+2х²=2(х²+3х+х+3)
7+2х²=2(х²+(3х+х)+3)
7+2х²=2(х²+4х+3)
7+2х²=2х²+8х+6
перенесём всё в правую часть и приравняем уравнение к нулю, при этом не забываем сменить знаки на противоположные
2х²+8х+6-7-2х²=0
группируем или приводим подобные члены
(2х²-2х²)+8х+(6-7)=0
8х-1=0
8х=1
х=1:8
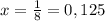
____________________________________________________
7+2·(0,125)²=2(0,125+1)(0,125+3) (это проверка)
7,03125=2·1,125·3,125
7,03125=7,03125
2) (y+4)(y+1)=y-(y-2)(2-y)
постепенно раскрываем скобки
у²+у+4у+4=y-(2y-y²-4+2y)
у²+у+4у+4=y-(-y²+(2y+2y)-4)
у²+у+4у+4=y-(-y²+4y-4)
у²+у+4у+4=y+y²-4y+4
перенесём всё в левую часть и приравняем уравнение к нулю, при этом не забываем сменить знаки на противоположные
у²+у+4у+4-y-y²+4y-4=0
группируем или приводим подобные члены
(у²-y²)+(у+4у-y+4y)+(4-4)=0
8у=0
у=0
(0+4)(0+1)=0-(0-2)(2-0)
4·1=0-(-2·2)
4=0-(-4)
4=0+4
4=4
2) Задача
Обозначим кроликов "к", а фазанов "ф"
у кроликов по 4 лапы, а у фазанов 2
согласно данным условия задачи составляем систему уравнениий:
4к+2ф=100 (1)
к+ф=36 (2)
к=36-ф
4(36-ф)+2ф=100
144-4ф+2ф=100
144-2ф=100
2ф=144-100
2ф=44
ф=44:2
ф=22 (шт.) - фазаны.
к=36-ф=36-22=14 (шт.) - кролики.
ответ: В клетке находятся 14 кроликов и 22 фазана.
5(3-5a)²-5(3a-7)(3a+7)=5(9-30а+25а²)-5(9а²-49)=45-150а+125а²-45а²+245=
(125а²-45а²)-150а+(45+245)=80а²-150а+290
(а+1)²+3(а-1)²-5(а+1)(а-1)=а²+2а+1+3(а²-2а+1)-5(а²-1)=а²+2а+1+3а²-6а+3-5а²+5=
(а²+3а²-5а²)+(2а-6а)+(1+3+5)=-а²-4а+9
(m-1)²-4(m+1)²-6(m+1)(m-1)=m²-2m+1-4(m²+2m+1)-6(m²-1)=m²-2m+1-4m²-8m-4-6m²+6=(m²-4m²-6m²)+(-2m-8m)+(1-4+6)=-9m²-10m+3
5(1-y)²-(3+y)²-3(1-y)(1+y)=5(1-2y+y²)-(9+6y+y²)-3(1-y²)=5-10y+5y²-9-6y-y²-3+3y²=
(5y²-y²+3y²)+(-10y-6y)+(5-9-3)=7y²-16y-7
5(1+m)(1-m)-(2-m)²-8(1-m)²=5(1-m²)-(4-4m+m²)-8(1-2m+m²)=5-5m²-4+4m-m²-8+16m-8m²=(-5m²-m²-8m²)+(4m+16m)+(5-4-8)=-14m²+20m-7
например , возьмем число 2
2 < 2^2 , потому что 2^2-- это 4
4> 2
возьмем число 1
1= 1^2 , потому что 1^2-- это 1
1=1
вот поэтому а《 а^2