Выражение: (а-2)(а-1)-а(а+1) главное, объсните как вы это ! по порядку

Question

Алгебра: Выражение: (а-2)(а-1)-а(а+1) главное, объсните как вы это ! по порядку

началось1939 · Accepted Answer

Пусть 100% - весь путь, который пройден со средней скоростью 50км/ч, тогда

х% - часть пути, которая пройдена со скоростью 45км/ч,

(100 - х)% - часть пути, которая пройдена со скоростью 60км/ч.

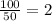$\frac{100}{50}=2$ - все время движения;

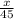$\frac{x}{45}$ - время, движения со скоростью 45 км в час;

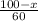$\frac{100-x}{60}$ - время, движения со скоростью 60 км в час.

Уравнение.

$\frac{x}{45} +\frac{100-x}{60} =2$

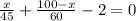
$\frac{x}{45} +\frac{100-x}{60} -2=0$

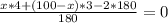
$\frac{x*4+(100-x)*3-2*180}{180} =0$

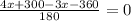
$\frac{4x+300-3x-360}{180} =0$

$\frac{x-60}{180} =0$

Дробь равна 0, если числитель равен нулю, значит:

x-60=0

x=60

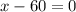
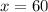
ответ: 60% пути он проехал со скоростью 45 км в час.

А можно и в частях:

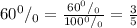
$60^0/_0=\frac{60^0/_0}{100^0/_0}=\frac{3}{5}$

ответ: $\frac{3}{5}$ пути он проехал со скоростью 45 км в час.