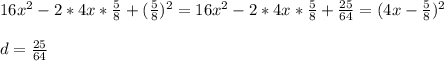
210=2·3·5·7, поэтому число 210 имеет 4 простых делителя. Каждый делитель числа 210 может быть разложен на простые множители, то есть задается набором простых делителей, выбранных из множества простых делителей числа 210. Поэтому число делителей числа 210 равно числу подмножеств этого множества, то есть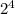 
, где 4 - это сколько элементов в этом множестве (то есть его мощность). При этом единице соответствует пустое подмножество.
Остается найти вероятность по формуле, которая работает в случае, когда все элементарные исходы равновероятны: вероятность события равна отношению числа благоприятных исходов к общему числу исходов:
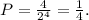
Для того, чтобы вычислить вероятность, сначала посмотрим на возможные исходы. Бросаем 2 монетки, значит могут быть следующие исходы:
1)на 1 монете выпадет ОРЕЛ, на второй ОРЕЛ
2)на 1 выпадет ОРЕЛ, на второй РЕШКА
3)на 1 выпадет РЕШКА, на второй ОРЕЛ
4)на 1 выпадет РЕШКА, на второй РЕШКА.
Больше исходов быть не может. Вспомнои формулу нахождения вероятности:
P=m/n, где m - благоприятные исходы, n - все исходы.
В нашем случае: Р=1 (потому что в перечисленных вышеискодах один раз выпадает два орла) / 4 (потому что мы посчитали, что исходов в даннной ситуации четыре)=0,25
ответ: 0,25
