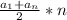Коэффициент подобия по определению считается по линейным размерам .
Для периметра (сумме линейных размеров) он равен k, для площадей k^2,
для объемов k^3.Тогда периметр равен 12*4=48 см, площадь равна 9*4^2=144 кв. см
Как-то так
Объяснение:
<!--c-->
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
P(ABC)P(RTG)=k20P(RTG)=19P(RTG)=9⋅20=180(см)
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
S(ABC)S(RTG)=k26S(RTG)=(19)26S(RTG)=181S(RTG)=6⋅81=486(см2)
Для начала найдем значение первого члена АП.
а1 = 7-3. а1=4.
Теперь найдем значение 12-го члена АП.
а12=7-3*12=-29.
S= (a1+a12)*6 = -25*6 = -150.
Для справки: S=