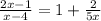
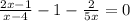
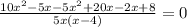
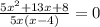
ОДЗ: 5x(x-4) ≠ 0 => x ≠ 0; x ≠ 4
5x² + 13x + 8 = 0
D = 13³ - 4·5·8 = 169 - 160 = 9 = 3² = (-3)²
x₁ = (-13-3)/10= -16/10= -1,6
x₁ = - 1,6
x₂ = (-13+3)/10= -10/10= -1
x₂ = - 1
ответ: {- 1,6; - 1}
1)возрастает на промежутке (-2;0) и (2;+inf)
2) (-inf;-2) и (0;+inf)
Объяснение:
1) находим производную и корни этой производной
f'(x) = 3x^3-12x
x(x^2-4) = =0
x = 0, x=2, x=-2
расположим эти корни на числовой прямой и подставим значения левее и правее найденных корней в нашу найденную производную
ищем промежутки в которых стоит + значит начиная от левого числа и до правого наша функция растет
2)аналогично первому, находим производную , приравниваем к нулю ищем корни выставляем на числовой прямой расставляем знаки и ищем + там где+ значит там функция растет
Пусть за х дней может закончить Катя, тогда еѐ производительность равна / х .
А за у дней может закончить Алиса, тогда еѐ производительность равна / у .
Т.к. они могут напечатать курсовую работу за 6 дней,
то /х + /у = 1/
Если сначала % = / части курсовой напечатает Катя,
а затем завершит работу Алиса, то Алисе остается
% = / части курсовой.
Вся курсовая работа будет выполнена за 12 дней т.е.
( /) х + (/ ) у = .
Решим систему:
/х + /у = / ,
(/) х + (/ ) у = .
+ = ,
+ = ;
у = − , ;
+ * ( − , ) = *( − , )
у = − , ;
, ² − + = ;
у = − , ;
² − + = ;
² − + = ;
= , у =
или = , у = . - не подходит, т.к. Катя печатает быстрее, чем Алиса.
Значит, Катя может напечатать курсовую работу за 10 дней.
ответ. за 10 дней
Решение приведено на фото