Алгебра: Из формулы x=3y/z вырозите примерную у

Из формулы x=3y/z вырозите примерную у

👇

Увидеть ответ

Ответ:

MikasaHasegava

19.01.2023

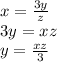
$x=\frac{3y}{z}\\3y=xz\\y=\frac{xz}{3}$

4,5(28 оценок)

Ответ:

daniilkrkrahmal

19.01.2023

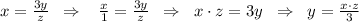
$x=\frac{3y}{z}\; \; \Rightarrow \; \; \; \frac{x}{1}=\frac{3y}{z}\; \; \Rightarrow \; \; x\cdot z=3y\; \; \Rightarrow \; \; y=\frac{x\cdot z}{3}$

4,5(68 оценок)

Открыть все ответы

Ответ:

lolkekpfff

19.01.2023

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. глава 5. решение треугольников 5.1. прямоугольный треугольник аксиомы 1.4 и 2.1 позволяли приписывать отрезкам и углам числа, равные их мерам, то есть измерять отрезки и углы. до сих пор не было связи между величинами углов и длинами отрезков. с введением треугольников появляется возможность связать величины градусных мер углов треугольника и длин его сторон. рассмотрим соотношения между сторонами и углами прямоугольного треугольника. 1 рисунок 5.1.1. прямоугольный треугольник. косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. пусть угол (bac) – искомый острый угол. так, например, для угла bac (рис. 5.1.1) теорема 5.1. косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника. доказательство пусть abc и a1b1c1 – два прямоугольных треугольника с одним и тем же углом при вершинах a и a1, равным α . построим треугольник ab2c2, равный треугольнику a1b1c1, как показано на рис. 5.1.2. это возможно по аксиоме 4.1. так как углы a и a1 равны, то b2 лежит на прямой ab. прямые bc и b2c2 перпендикулярны прямой ac, и по следствию 3.1 они параллельны. по теореме 4.13 2 рисунок 5.1.2. к теореме 5.1. но по построению ac2 = a1c1; ab2 = a1b1, следовательно, что и требовалось доказать. теорема 5.2. теорема пифагора. в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. модель 5.2. доказательство теоремы пифагора. на рисунке 5.1.3 изображен прямоугольный треугольник. bc и ac – его катеты, ab – гипотенуза. по теореме bc2 + ac2 = ab2. доказательство пусть abc – данный прямоугольный треугольник с прямым углом при вершине c. 3 рисунок 5.1.3. к доказательству теоремы пифагора. проведем высоту cd из вершины c. по определению из треугольника acd и из треугольника abc. по теореме 5.1 и, следовательно, . аналогично из δ cdb, из δ acb, и отсюда ab · bd = bc2. складывая полученные равенства и, замечая, что ad + bd = ab, получаем ac2 + bc2 = ab · ad + ab · bd = ab (ad + bd) = ab2. теорема доказана. в прямоугольном треугольнике любой из катетов меньше гипотенузы. косинус любого острого угла меньше единицы. пусть [bc] – перпендикуляр, опущенный из точки b на прямую a, и a – любая точка этой прямой, отличная от c. отрезок ab называется наклонной, проведенной из точки b к прямой a. точка c называется основанием наклонной. отрезок ac называется проекцией наклонной. с теоремы пифагора можно показать, что если к прямой из одной точки проведены перпендикуляр и наклонные, то любая наклонная больше перпендикуляра, равные наклонные имеют равные проекции, из двух наклонных больше та, у которой проекция больше. синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. по определению тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. для угла (bac) прямоугольного треугольника, изображенного на рис. 5.1.1, имеем так же как и косинус, синус угла и тангенс угла зависят только от величины угла. 4 рисунок 5.1.4. из данных определений получаем следующие соотношения между углами и сторонами прямоугольного треугольника: если α – острый угол прямоугольного треугольника, то катет, противолежащий углу α , равен произведению гипотенузы на sin α; катет, прилежащий к углу α , равен произведению гипотенузы на cos α; катет, противолежащий углу α , равен произведению второго катета на tg α.

4,5(96 оценок)

Ответ:

muzaka

19.01.2023

алгебраический

х – скорость течения реки

6х - собственная скорость крокодила

6х + х = 7х - скорость крокодила по течению реки

6х - х = 5х - скорость крокодила против течения реки

7х + 5х = 12х – скорость сближения на расстоянии 924 км

924 : 7 = 132 км/ч - скорость сближения на расстоянии 924 км

Уравнение

12х = 132

х = 132 : 12

х = 11 км/ч - скорость течения реки

5х + х = 6х - скорость сближения на расстоянии 308 км

11 * 6 = 66 км/ч - скорость сближения на расстоянии 308 км

308 : 66 = 14/3 = 4целых 2/3 = 4 ч 40 мин
ответ: 4 ч 40 мин

арифметический
1) 924 : 7 = 132 км/ч - скорость сближения на расстоянии 924 км
2) 132 : 2 = 66 км/ч - собственная скорость крокодила
3) 66 : 6 = 11 км/ч - скорость течения реки (она же скорость плота)
4) 66 - 11 = 55 км/ч - скорость крокодила против течения реки
5) 55 + 11 = 66 км/к - скорость сближения на расстоянии 308 км
6) 308 : 66 = 14/3 = 4целых 2/3 = 4 ч 40 мин
ответ: 4 ч 40 мин

4,6(35 оценок)

Это интересно:

Образование-и-коммуникации

22.08.2020

Как написать миф: вдохновляющая сила древних легенд...

Взаимоотношения

26.10.2021

Мы все должны уважать и почитать своих родителей. Но как это сделать?...

Компьютеры-и-электроника

14.05.2023

Как создать свою видеоигру с нуля: от идеи до релиза...

31.05.2021