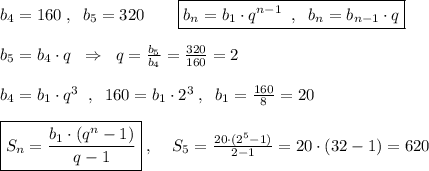
Объяснение:
1) x^2- 4x - 32 = x^2 + 4x - 8x - 32 = x ( x+4) - 8( x+4) = (x+4)×(x-8)
2)4x^2 - 15x + 9 = 4x^2 - 3x - 12x + 9 = x(4x-3) - 3( 4x-3) = (4x-3) × (x-3)
2.
х км/ч - скорость течения
15-х км/ч - скорость против течения
15+х км/ч - скорость по течению
72/(15-х) - 72/(15+х) = 2
72(15+х)-72(15-х)=2(225-х^2)
72(15+х-15+х)=2(225-х^2)
36*2х=225-х^2
х^2+72х-225=0
х=-75 - не удовлетворяет условию задачи
х=3 (км/ч) - скорость течения
1. x^4-8x^2 - 9 = 0
Решаем заменой переменной x^2 = t
t^2 -8t -9=0
Дискрминант и все дела
t (1)=-1 ; t(2) = 9
Потом подставляем и считаем
x^2 = -1
x^2 = 9
Ну и в конце
x ∉ R
x = -3
x = 3
ответ : x (1) = - 3 ; x(2 ) = 3
2. ОДЗ : x ≠ -2
Когда знаминатели равны , то мы можем числа прировнять и выходит
x^2 - 7x = 18
x^2 - 7x -18 = 0
x^2 + 2x - 9x - 18 = 0
x( x+2) - 9 ( x+ 2) = 0
( x+2) × ( x -9 ) = 0
x = -2
x = 9
ответ : x = 9

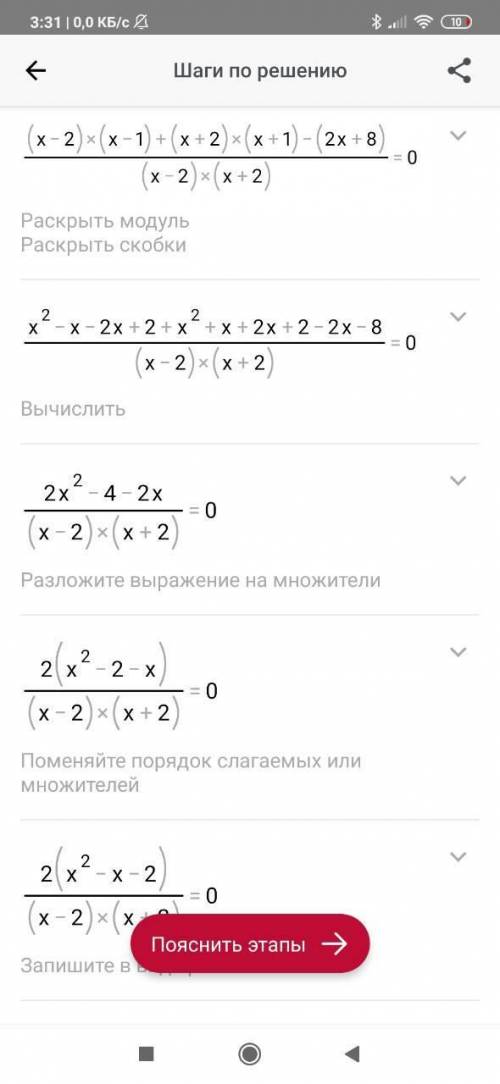
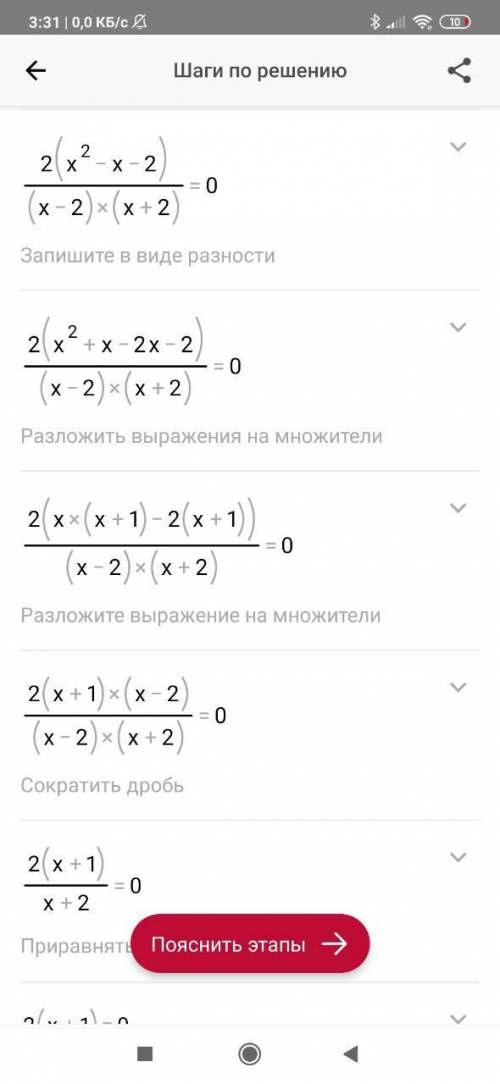

1) ветви направлены вверх, вершина(2;-1)
3) Ветви направлены вверх, вершина (1;6)
6) ветви направлены вверх, вершина(3;-10)
вершина рассчитывала по формуле; m= -в/2а(это х);n= подставляешь значения х в квадратное уравнение и находишь у. Пересечение параболы с осями координат это нули функции, для их нахождения надо решить квадратное уравнение через дискриминант т.е приравниваешь уравнение к нулю и решаешь по формуле D = b^2-4ac(должно получиться число в квадрате, в редких случаях рашается с корнем)и x1,2 = -b±√D/2а