1. Интегрирование ведется по множеству 0 < x < 1, 0 < y < √(2x-x^2)
√(2x - x^2) принимает значения от 0 (x = 0) до 1 (x = 1), так что множество интегрирования является частью множеста 0 < x < 1, 0 < y < 1, где выполняется y < √(2x - x^2)
0 < y < √(2x - x^2) при 0 < x < 1 эквивалентно 0 < y^2 < 2x - x^2 = 1 - (1 - 2x + x^2) = 1 - (x-1)^2
т.е. (x-1)^2 < 1 - y^2
|x - 1| = 1 - x < √(1 - y^2)
x > 1 - √(1 - y^2)
ответ: интеграл от 0 до 1 по dy интеграл от 1 - √(1-y^2) до 1 f(x,y) по dx
2. 0 < y < 1, -√(1-y^2) < x < 1-y
-√(1-y^2) принимает значения от -1 (y = 0) до 0 (y = 1)
1 - y принимает значения от 0 (y = 1) до 1 (y = 0)
Т.е. область интегрирования: -1 < x < 1, 0 < y < 1, где одновременно -√(1-y^2) < x и x < 1-y
x < 1 - y ~ y < 1 - x
-√(1-y^2) < x :
1) При x > 0 - любой y (от 0 до 1)
2) При x < 0:
√(1-y^2) > (-x) > 0
1 - y^2 > x^2
0 < y^2 < 1 - x^2
0 < y < √(1 - x^2)
Т.е. исходные условия эквивалентны тому, что:
при x >= 0: y < 1 - x
при x < 0: одновременно y < √(1 - x^2) и y < 1 - x, но т.к. √(1 - x^2) <= 1 - x при x < 0, достаточно условия y < √(1 - x^2)
ответ: (интеграл от -1 до 0 по dx интеграл от 0 до √(1 - x^2) f(x,y) по dy) + (интеграл от 0 до 1 по dx интеграл от 0 до 1 - x f(x,y) по dy)
Или, что то же самое, интеграл от -1 до 1 по dx от 0 до min{ 1 - x, √(1 - x^2) } f(x,y) по dy




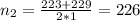
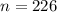
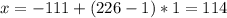
1) (а/7-b/6)-(З×5/6 - с/6) ( выносим общие множители)
1/42(6а-42×b/6) -1/6×(3×5-6×с/6) (сокращаем)
1/42(6а-7b)-1/6(15-с)
1/42(6а-7б-7(15-с)) (раскроем скобки)
1/42(6а-7б-105+7с) упростили
теперь подставляем
1/42(6×37-7×13-105+7×7)
75×1/42=75/42= 1(целая)×33/42