Объяснение:
1.
a8=a7+d
d=a8
a8=a7+a8=>a7=0
2.
a1 = -12
a2 = -9
an = a1 + d * (n - 1);
a2 = a1 + d;
a2 - a1 = d.
d = -9 - (-12) = 3.
a8 = a1 + 7 * d;
a8 = -12 + 7 * 3;
a8 = 9.
S8 = (a1 + a8) * 8/2;
S8 = 4 * (-12 + 9);
S8 = -12.
3.
A6=a1+d(6-1), a7=a1+d(7-1), a11=a1+d(11-1), a12=a1+d(12-1).
(a1+6d)+(a1+d11)+8=(a1+5d)+(a1+10d)
a1+6d+a1+11d+8=aq+5d+a1+10
17d+8=15d
2d=-8
d=-4
4.
q=4/12=1/3
b9=12/1/3=36
5.
a1=a3:q²
a1=36:9
a1=4
s5=a1.q^4
s5=4.3^4, s5=4.81, s5=324
6.
a8=a7*q=a7*a8
a7=a8/a8=1
7.
A5=a1*q^4
Q^4=5
A13=a1*q^12=a5*q^8
A13/a5=q8=25
8.
an = a1 + (n - 1)d;
an = 6 + 4(n - 1);
an > 260;
6 + 4(n - 1) > 260;
4(n - 1) > 260 - 6;
4(n - 1) > 254;
n - 1 > 254/4;
n - 1 > 63,5;
n > 63,5 + 1;
n > 64,5;
9.
A1=6
a6=17
a2, a3, a4, a5-?
a6=a1+5d
d = (a5-a1) / 5
d = (17-6) / 5=11/5=2,2
a2=a1+d=6+2,2=8,2
a3=a2+d=8,2+2,2=10,4
a4=a3+d=10,4+2,2=12,6
a5=a4+d=12,6+2,2=14,8
10.
а1=60
аn=110
N=51
(2*60+50)*51/2=4335
11.
Sn = b1 * (1 - qn)/(1 - q).
S4 = b1 * (1 - (- 3)4)/(1 - (- 3)) = - 40.
b1 = (- 40) : (1 - 81)/(1 + 3) = - 40 * 4/(- 80) = 2.
S8 = b1 * (1 - (- 3)8)/(1 - (- 3)) = 2 * (1 - 6561)/4 = - 6560/2 = - 3280.
13.
аn=1+7*(n-1)=1+7n-7= 7n-6
28+6=34
55+6=61
9156:7=1308
14.
a2=a1+d; 4=a1+d
a28=a1+27d; 56=a1+27d
a28-a2=56-4=52
52=26d
d=2
S28=(2a1+d(n-1))/2 s=(4+54)/2=29
a2=4=a1+d,то a1=2
15.
a6=a1+5d
a10=a1+9d
a16=a1+15d
а10-а6=4d
а10-а6=20-14=6
d=1.5
а16 и а10:
а16-а10=6d
28-20=8
d=8/6=4/3
d разные получаются - значит числа не принадлежат арифметической прогрессии
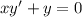
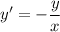 - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными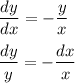
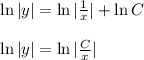
 - общее решение
- общее решение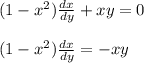

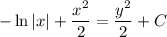 - общий интеграл
- общий интеграл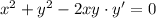

 , тогда
, тогда 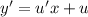



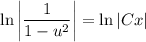
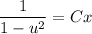
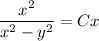 - общий интеграл
- общий интеграл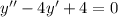
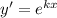 , тогда будем иметь характеристическое уравнение следующего вида:
, тогда будем иметь характеристическое уравнение следующего вида:
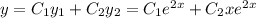 - общее решение
- общее решение
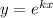 , тогда получаем
, тогда получаем
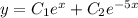

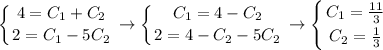
 - частное решение
- частное решение
(x+y)(y-9)
(-1-c)(b-a)