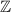разделим на три класса:
, где + обозначает операцию объединения и изначает, что множества 
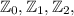дисъюнктны.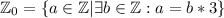
.
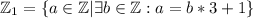
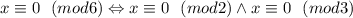
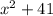делится на два (сумма нечетных чисел четна), то есть выражение все равно делится на два, первое условие выполнено. Докажем, что x делится на 3:
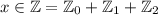, то рассмотрим три случая:
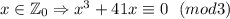так как 
.
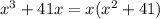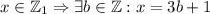
для каких-то 
, то есть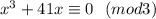 
.
.
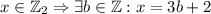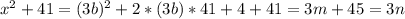для каких-то , то есть .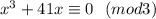
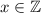выражение 
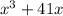делится на 6.
Объяснение:
Чтобы задать функцию нужно найти закономерность (формулу) перехода от координаты х к координате у
1) 1 таблица
1⇒1*3=3
2⇒2*3=6
3⇒3*3=9
4⇒4*3=12
Легко видеть что идет умножение на число 3
тогда функция будет иметь вид y=3x
2) 2 таблица
все значения "у" отличаются от первой таблицы на 1
значит надо просто к "формуле" добавить 1
тогда функия будет иметь вид y=3x+1
3) 3 таблица
все значения "у" отличаются от первой таблицы на 1 (только теперь меньше)
значит надо просто из "формуле" вычесть 1
тогда функия будет иметь вид y=3x-1
4) 4 таблица
все значения "у" отличаются от первой таблицы на "знак"
значит надо просто первую формулу сделать отрицательной
тогда функия будет иметь вид y= -3x
5) 5 таблица
все значения "у" отличаются от четвертой таблицы на 1 (больше)
значит надо просто к 4 "формуле" добавить 1
тогда функия будет иметь вид y= -3x+1
6) 6 таблица
А вот тут линейной закономерности не будет .
Это легко видеть на рисунке (см. приложение)
Вывод: по данной таблице задать функцию нельзя
Если бы в таблице стояли значения
1⇒ -4
2⇒-7
3⇒-10
4⇒-13
То функция имела бы вид у= -3х-1
ответ:2 пример
1 ) 4,78
2 ) -8
ответ:3 пример
1)
8
3
15
2)
11
- 3
50
Объяснение:
4- Мне лень))