в) Предположим, нам удалось вычеркнуть n сумм.
С одной стороны, сумма всех вычеркнутых чисел не меньше 1 + 2 + 3 + ... + 3n = 3n (3n + 1)/2; с другой стороны, сумма вычеркнутых чисел не больше 39 + 38 + 37 + ... + (40 - n) = n (79 - n) / 2. Поэтому n (79 - n) / 2 ≥ 3n (3n + 1)/2; 79 - n ≥ 9n + 3; n ≤ 7.
Покажем, что n = 7 возможно:
1 + 15 + 23 = 39
2 + 14 + 22 = 38
3 + 13 + 21 = 37
4 + 12 + 20 = 36
5 + 11 + 19 = 35
6 + 10 + 18 = 34
7 + 9 + 17 = 33
а) Например, первые 6 примеров выше
б) Нет, по доказанному
ответ. б) нет; в) 7
Наиболее сложное решение:
Пусть x - количество бензина в первой бочке, а y - во второй. По условию задачи составим систему уравнений:
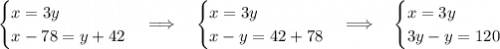
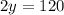
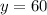 (л) - бензина во второй бочке
(л) - бензина во второй бочке
60 · 3 = 180 (л) - в первой бочке
Решение через уравнение (рационально):
Пусть x - количество бензина во второй бочке, тогда в первой - 3x. По условии задачи составляем уравнение:
3x - 78 = x + 42
3x - x = 42 + 78
2x = 120
x = 60 (л) - во второй бочке
60 · 3 = 180 (л) - в первой бочке
ответ: в первой бочке 180 л бензина, во второй - 60 л.
Задача может быть простой, даже несмотря на тему (здесь нельзя решить сложнее, чем в первом варианте)
второе ур-ние домножаем на -1 и складываем с первым.
4х - 3х + у - у = 30 - 28
х = 2
у = 22