Алгебра: 7/√3-√х избавьтесь от иррациональной дроби

(см. объяснение)Объяснение:Шаг 1: преобразуем уравнение.Шаг 2: выполним замену.Замена:ОДЗ для буквы t:Sin дает значения от -1 до 1 включительно. Если умножить их на , то получится, что ,Шаг 3: решим квадратное уравнение.Продолжим решение:Рассмотрим корень (а вообще понятно, что само число больше, чем корень из него, а тут мы еще корень из 10 вычитаем). Он посторонний, так как выше мы доказали, что . Другой корень посторонним не является. Значит работать будем только с ним.Шаг 4: обратная замена.Обратная...

7/√3-√х избавьтесь от иррациональной дроби

👇

Увидеть ответ

Ответ:

ketrindemey5

29.11.2020

7/(√3-√х) = [7*(√3+√х)] / [(√3 - √х)*√3 + √х)] =

= [7*(√3 + √х)] / [(√3)² - (√х)²] = [7*(√3 + √х)] / (3 - x)

4,4(66 оценок)

Открыть все ответы

Ответ:

Дашундель

29.11.2020

3) Первый предел равен нулю, т.к. знаменатель быстрее стремится к бесконечности. И есть правило, если х стремится к бесконечности, то смотрим на стандартный вид многочленов числителя и знаменателя, если степень многочлена, стоящего в числителе выше, чем степень многочлена знаменателя, то ответ бесконечность, если ниже, то нуль, у нас как раз этот случай, а если показатели степеней равны, то ищем при максимальных одинаковых показателях отношение коэффициентов.

6) Во втором пределе если подставить 3, числитель обратится в нуль, ровно как и знаменатель, эту неопределенность устраняют разложением числителя на множители (х-3)(х²+3х+9²)/(х-3) и сокращением на (х-3), тогда после сокращения получим 3²+3*3+9=27

9) У третьего предела такая же беда. Разложим по формуле числитель и вынесем за скобку общий множитель из знаменателя, убираем неопределенность путем сокращения дроби.

(х-1)²/(х*(х-1)(х+1))=(х-1)/(х*(х+1))=(1-1)/(1*2)=0

ответ 3) 0

6)27

9) 0

4,8(67 оценок)

Ответ:

yoc

29.11.2020

(см. объяснение)

Объяснение:

Шаг 1: преобразуем уравнение.

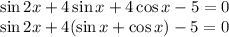
$\sin2x+4\sin x+4\cos x-5=0\\\sin 2x+4(\sin x+\cos x)-5=0$

Шаг 2: выполним замену.

Замена:

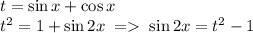
$t=\sin x+\cos x\\t^2=1+\sin 2x\; =\; \sin 2x=t^2-1$

ОДЗ для буквы t:

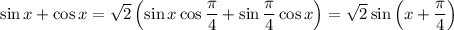
$\sin x+\cos x=\sqrt{2}\left(\sin x\cos\dfrac{\pi}{4}+\sin \dfrac{\pi}{4}\cos x\right)=\sqrt{2}\sin\left(x+\dfrac{\pi}{4}\right)$

Sin дает значения от -1 до 1 включительно. Если умножить их на 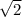$\sqrt{2}$ , то получится, что $t\in\left[-\sqrt{2};\; \sqrt{2}\right]$ ,

Шаг 3: решим квадратное уравнение.

Продолжим решение:

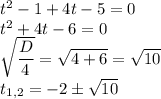
$t^2-1+4t-5=0\\t^2+4t-6=0\\\sqrt{\dfrac{D}{4}}=\sqrt{4+6}=\sqrt{10}\\t_{1,2}=-2\pm\sqrt{10}$

Рассмотрим корень 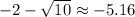$-2-\sqrt{10}\approx-5.16$ (а вообще понятно, что само число больше, чем корень из него, а тут мы еще корень из 10 вычитаем). Он посторонний, так как выше мы доказали, что $t\in\left[-\sqrt{2};\; \sqrt{2}\right]$ . Другой корень посторонним не является. Значит работать будем только с ним.

Шаг 4: обратная замена.

Обратная замена:

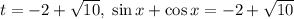
$t=-2+\sqrt{10},\; \sin x+\cos x=-2+\sqrt{10}$

Выше уже узнавали значение суммы sin и cos через одну тригонометрическую функцию. Поэтому пишу сразу:

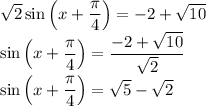
$\sqrt{2}\sin\left(x+\dfrac{\pi}{4}\right)=-2+\sqrt{10}\\\sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{-2+\sqrt{10}}{\sqrt{2}}\\\sin\left(x+\dfrac{\pi}{4}\right)=\sqrt{5}-\sqrt{2}\\$

Полученное уравнение можно без труда решить следующим образом:

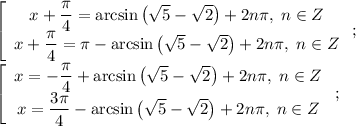
$\left[\begin{array}{c}x+\dfrac{\pi}{4}=\arcsin\left(\sqrt{5}-\sqrt{2}\right)+2n\pi,\; n\in Z\\x+\dfrac{\pi}{4}=\pi-\arcsin\left(\sqrt{5}-\sqrt{2}\right)+2n\pi,\; n\in Z\end{array}\right;\\\left[\begin{array}{c}x=-\dfrac{\pi}{4}+\arcsin\left(\sqrt{5}-\sqrt{2}\right)+2n\pi,\; n\in Z\\x=\dfrac{3\pi}{4}-\arcsin\left(\sqrt{5}-\sqrt{2}\right)+2n\pi,\; n\in Z\end{array}\right;$

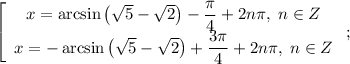
$\left[\begin{array}{c}x=\arcsin\left(\sqrt{5}-\sqrt{2}\right)-\dfrac{\pi}{4}+2n\pi,\; n\in Z\\x=-\arcsin\left(\sqrt{5}-\sqrt{2}\right)+\dfrac{3\pi}{4}+2n\pi,\; n\in Z\end{array}\right;$