Выражение под корнем должно быть неотрицательным, знаменатель должен быть ненулевым.
То есть x - 3 >= 0 и x^2 + 25 ≠ 0.
x - 3 >= 0 ⇔ x >= 3
x^2 + 25 выполняется при любых x
Получаем: [3; +∞)
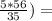log₂8 = 3
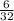= log₂(
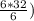= log₂32 = 5
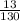= lg
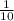= -1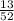
)⁵ = (log₂
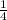)⁵ = (-2)⁵ = -32
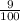)⁴ = (log₀.₃0.09)⁴ = 2⁴ = 16
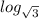log₅125 = 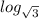3 = 2
Чтобы найти область определения функции надо искать в первую очередь, не может ли знаменатель быть нулем, вторая опасность - отрицательное число под знаком кв. корня.
1) знаменатель есть: x²+25; x²≥0, x²+25>0 при любых значениях ( х ).
2) корень: х-3≥0; х≥3
ответ: ОДЗ х∈[3;+∞).