Составить все эти уравнения по картинке и решить их. ps я их составил, но какие числа в них подставлять я без понятия. заранее y=kx +b x²+y²=r² y=(x-6)²
Уравнение прямой, проходящей через точки ( -5,-2) и (-2,0) имеет вид y=kx+b:
Уравнение окружности с центром в точке и радиусом, равным R, имеет вид: .
Тогда окружность на рисунке имеет вид:
Если перед корнем берём знак (+), то получаем уравнение верхней полуокружности (y≥0) , а если берём знак (-), то получаем уравнение нижней полуокружности (у≤0) .
Уравнение прямых, проходящих параллельно оси ОХ через точку с координатами (a,b) , имеет вид: у=b .
Аналитически заданная на графике функция имеет вид:
Решение: Из теоремы Пифагора мы знаем, что в прямоугольном треугольнике: с^2=a^2+b^2, можно найти стороны катетов. Для этого один из катетов пусть будет обозначен а, а второй: b= а+2, подставим данные этой задачи и найдём катеты этого. 10^2=a^2+(a+2)^2 100=a^2+a^2+4a+4 Решим данное уравнение: 2a^2+4a-96=0 приведём это квадратное уравнение к простомц квадратному уравнению, разделив его на 2, a^2+2a-48=0 a1,2=-1+-sqrt(1+48)=-1+-7 a1=-1+7=6 a2=-1-7=-8 (не соответствует условию задачи) Второй катет b=6+2=8
То́ждество — это равенство, выполняющееся на всём множестве значений входящих в него переменных. Чтобы доказать тождество надо выполнить тождественные преобразования одной или обеих частей равенства, и получить слева и справа одинаковые выражения. Чтобы доказать, что равенство не является тождеством, достаточно найти одно допустимое значение переменной, при котором, получившиеся числовые выражения не будут равны друг другу.
1) ( -m-n)^2=(m-n)^2 m^2+2mn+n^2= m^2-2mn+n^2 - не тождественно равное выражение.
( -m-n)^2=(m+n)^2 m^2+2mn+n^2= m^2+2mn+n^2 -тождественно равное выражение
2) (-m+n)^2=(m-n)^2 m^2-2mn+n^2=m^2-2mn+n^2 - тождественно равное выражение
Уравнение прямой, проходящей через точки ( -5,-2) и (-2,0) имеет вид y=kx+b:
Уравнение окружности с центром в точке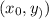 и радиусом, равным R, имеет вид:
и радиусом, равным R, имеет вид: 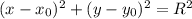 .
.
Тогда окружность на рисунке имеет вид:
Если перед корнем берём знак (+), то получаем уравнение верхней полуокружности (y≥0) , а если берём знак (-), то получаем уравнение нижней полуокружности (у≤0) .
Уравнение прямых, проходящих параллельно оси ОХ через точку с координатами (a,b) , имеет вид: у=b .
Аналитически заданная на графике функция имеет вид: