1) 2синус x/2 косинус 5к-косинус х = 0 2) tg(30°-х)=√3 3) косинус(π/4-2х)= -1 4) tg(4х-π/6)=√3/3

👇

Ответ:

lady198026

11.05.2021

Под 3 только знаю сорян(
1) 2синус x/2 косинус 5к-косинус х = 0 2) tg(30°-х)=√3 3) косинус(π/4-2х)= -1 4) tg(4х-π/6)=√3/3

4,7(62 оценок)

Открыть все ответы

Ответ:

Максим111136322

11.05.2021

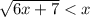
1) $\sqrt{6x+7} < x$

Составим систему неравенств, учитывая каждое ограничение, накладывающееся на аргумент:

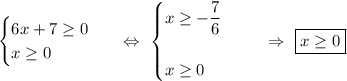
$\begin{equation*}\begin{cases}6x + 7 \geq 0\\x \geq 0\end{cases}\end{equation*}\ \ \ \Leftrightarrow\ \begin{equation*}\begin{cases}x \geq -\dfrac{7}{6}\\\\x \geq 0\end{cases}\end{equation*}\ \ \ \ \ \Rightarrow\ \boxed{x\geq 0}$

Теперь продолжаем решать наше неравенство.

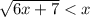
$\sqrt{6x+7} < x$

Возведём обе части неравенства в квадрат.

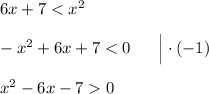
$6x + 7 < x^2\\\\-x^2 + 6x + 7 < 0\ \ \ \ \ \Big| \cdot (-1)\\\\x^2 - 6x - 7 0$

Получаем квадратное неравенство. Чтобы найти нули, приравняем левую часть к 0 и найдём корни квадратного уравнения.

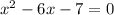
x^2 - 6x - 7 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}x_{1}x_{2} = -7\\x_{1} + x_{2} = 6\end{cases}\end{equation*}\ \ \ \ \ \Big| x = 7; x = -1$

Возвращаемся к неравенству:

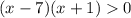
(x-7)(x+1) 0

Решим его методом интервалов.

Нули: 7; -1.

+ - +

---------------------о------------------------------о-----------------------> х

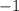
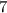
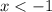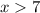Получаем, что решением квадратного неравенства являются промежутки x < -1 и x 7 . Но не забываем про ограничение 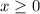$x \geq 0$ , которое мы вычислили выше.

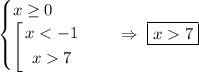
$\begin{equation*}\begin{cases}x\geq 0\\$\left[\begin{gathered}x < -1\\x 7\end{gathered}\end{cases}\end{equation*}\ \ \ \ \Rightarrow\ \boxed{x 7}$

ответ: 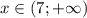$x \in (7;+\infty)$ .

2) $(x-2)^2(x^2-4x+3)\geq 0$

Это задание можно решить методом интервалов. Нужно найти нули. С левым множителем понятно, он обращается в 0 при 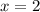x = 2 . Приравняем правый множитель к нулю, чтобы найти его корни.

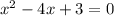
x^2 - 4x + 3 = 0

По теореме Виета:

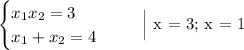
$\begin{equation*}\begin{cases}x_{1}x_{2} = 3\\x_{1} + x_{2} = 4\end{cases}\end{equation*}\ \ \ \ \ \Big| x = 3; x = 1$

Применяем метод интервалов для нашего неравенства.

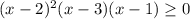
$(x-2)^2(x-3)(x-1) \geq 0$

Нули: 1; 2; 3.

+ - - +

--------------- $\bullet$ --------------------- $\bullet$ --------------------- $\bullet$ -------------------> x

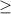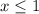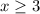Так как знак неравенства $\geq$ , то нам нужны те промежутки где стоит знак +. Таких два: $x \leq 1$ и $x \geq 3$ , но и это ещё не всё. Есть ещё точка 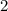, и она тоже является решением, поскольку при ней выражение обращается в 0.

ответ: $(-\infty; 1] \cup [3; +\infty) \cup \left \{2\right \}$ .

4,6(96 оценок)

Ответ:

Valya1873

11.05.2021

по камерам увидел что вы ночью занимаетесь ли вы в курсе что это за что не так я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении нн я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать во вложении я не могу писать

4,7(89 оценок)

Это интересно:

Компьютеры-и-электроника

17.04.2020

Создание онлайн веб каста с помощью Windows Media Encoder...

Транспорт

14.01.2023

Как избежать аварий на дороге...

Компьютеры-и-электроника

18.09.2022

Как добавить кнопку Facebook на свой сайт: шаг за шагом...

Компьютеры-и-электроника