1) -15х-25у=-5(3х+5у)
2) 48с+36q=6(8c+6q)
3) 13a-13=13(a-1)
4) 4x³+2=2(2x³+1)
5) -10-5a=-5(2+a)
6) 4ab+6ac=2a(2b+3c)
7) 2a-8ab=2a(1-4b)
8) 7y²-49y=7y(y-7)
9) -5x³+15x²=-5x²(x-3)
10) a²b⁴-ab³=ab³(ab-1)
Пусть боковая сторона равнобедренного треугольника - х см, тогда основание треугольника будет 18-2х или 2(9-х) см.
Составим выражение для высоты треугольника, проведенной к основанию
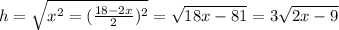
Теперь составим выражение площади треугольника

Найдем производную полученного выражения

при x<6 значение производной S'>0, а при x>6 S'<0, значит при х=6 функция S принимает максимальное значение (максимум функции)
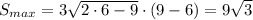
Таким образом, плащадь треугольника будет наибольшей, если все его стороны будут равны 6 см, т.е. он будет равносторонним.
ответ:1)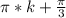
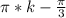
2) НЕТ ДЕЙСТВИТЕЛЬНЫХ РЕШЕНИЙ
Второе даже решать не буду там и так ясно что нет решений а первое вот:
1)разложи косинус получишь
4 sin^4 x = 5-5*sin^2(x) + 1
2)заменяем sin^2 x=t
-1<t<1
4*t^2=5-5*t+1
4*t^2+5t-6=0
t=-2 t=3/4 (по т.виета)
||
\/
sin^2 x=-2 sin^2 x = 3/4
нет решений
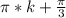
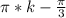
т.к. sinx=корень из 3/ 2
тк -1<sinx<1 x=arcsin( корень из 3/ 2)+pi*k
x=-arcsin( корень из 3/ 2)+pi*k
arcsin( корень из 3/ 2)=pi/3
отсуда
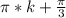
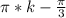
1) -15x-25y= 5(-3x-5y)
2) 48c+36q=12(4c+3q)
3) 13a-13=13(a-1)
4) 4x^3 + 2 = 2(2x^3 + 1)
5) -10-5a= 5(-2-a)
6) 4ab+6ac= 2a(2b+3c)
7) 2a-8ab= 2a(1-4b)
8)7y^2 - 49y= 7y( y -7)
9) -5x^3 + 15x^2 = 5x^2( -x+ 3)
10) a^2 * b^4 - ab^3= ab^3( a*b - 1)