ответ: \frac{4x^4-4x^3+x^2}{-2x^2+5x-2}+ \frac{2x^3-7x^2+5x+1}{x-2}\leqslant0
ОДЗ:
-2x^2+5x-2\neq0\\ 2x^2-5x+2\neq0\\ D=25-16=9; \sqrt {D}=3 x_{1/2}\neq0 x_1\neq \frac{1}{2}; \ \ x_2\neq2
-2x^2+5x-2=-(x-2)(2x-1)=(2-x)(2x-1)
\frac{x^2(4x^2-4x+1)}{(2-x)(2x-1)}+ \frac{2x^3-7x^2+5x+1}{x-2}\leqslant0 \frac{x^2(2x-1)^2}{(2-x)(2x-1)}+ \frac{2x^3-7x^2+5x+1}{x-2}\leqslant0 \frac{2x^3-7x^2+5x+1}{x-2}- \frac{x^2(2x-1)}{x-2}\leqslant0 \frac{2x^3-7x^2+5x+1-2x^3+x^2}{x-2}\leqslant0 -6x^2+5x+1\leqslant0 6x^2-5x+1=0\\ D=25+24=49; \ \sqrt D=7 x_{1/2}= \frac{5\pm7}{12} x_1=- \frac{1}{6};\ \ x_2=1
__+__- \frac{1}{6} __-__ \frac{1}{2} __-__1__+__2__-__
ответ: x\in [- \frac{1}{6}; \frac{1}{2})\bigcup (\frac{1 }{2};1]\bigcup(2;+\infty)
Объяснение:
1. Табличка во вложении:
4Гб - апрель
1Гб - июль
3Гб - июнь
5Гб - нет
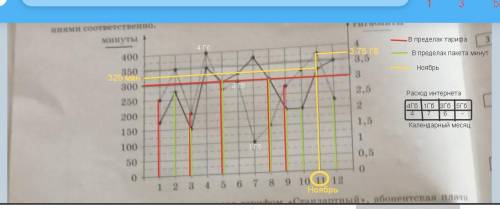
2. Расходы за ноябрь (11месяц):
Стоимость услуги связи = 400 руб.,
Превышение лимита минут:
лимит - 300 мин., израсходовано - 325 мин.
цена минуты сверх лимита - 2.5 р/мин.,
325-300=25 мин. сверх лимита;
25*2.5=62.5 руб. - за превышение лимита минут.
Превышение пакета инета:
Пакет = 3Гб;
Израсходовано - 3.75ГБ;
3.75-3=0.75Гб сверх лимита.
Превышение лимита по инету - 0.5Гб=80 руб.,
0.75*80=120 руб. за превышение лимита инетаю
Всего: 400+62.5+120=582.5 руб. оплачено за ноябрь
3. Не превышал лимит по пакету минут: 7 мес.
4. Не превышал лимит по пакетам минут и инета: 5 мес.
График во вложении
6. Решение задания приложено