1) (х²+3у)²=x⁴+6x²y+9y²
2) (0,3а²+4b)²=0.09a⁴+2.4a²b+16b²
3) (0,2m²-5n)²= 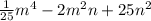
4) (1,3p³+2,5p²)²= 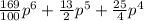
5) (2,4c³-1,5d²)² = 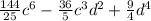
6) (7x²y+3xy²)² = 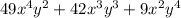
task/29465133
√3sinx + cosx = 2
* * * методом вс угла: asinx + bcosx=√(a²+b²)sin(x+φ) , где
φ= arctg(b/a) || a =√3 ; b =1 ; √(a²+b²)= 2 ; φ= arctg(1/√3)=π/6 || * * *
но уравнение проще √3sinx + cosx = 2 ⇔ √3)/2 *sinx +(1/2)* cosx =1 ⇔
sinx*cos(π/6) +cosx*sin(π/6) =1 ⇔ sin(x +π/6) =1 ⇔x+π/6=π/2+2πn , n∈ ℤ .⇔
ответ : x =π/3+2πn , n∈ ℤ.
как не надо решать ( однородное уравнение)
* * * sin²α+cos²α=1 ; sin2α=2sinαcosα ; cos2α= cos²α - sin²α ; x =2*(x/2) * * *
√3sinx +cosx=2⇔2√3sin(x/2)cos(x/2)+cos²(x/2)-sin²(x/2)=2cos²(x/2)+2sin²(x/2)
⇔ 3sin²(x/2) -2√3sin(x/2)cos(x/2 +cos²(x/2) =0 || : cos²(x/2) ≠ 0
3tg²(x/2) - 2√3tg(x/2) +1 =0 кв. уравнение относительно tg(x/2) = t
D₁ =(√3)²-3*1=0 кратный корень
tg(x/2) = (√3)/3 * * * x /2 =arctg[(√3)/3] +πn , n ∈ ℤ * * *
tgx =tg[2*(x/2) ] = 2tg(x/2) / [ 1 - tg²(x/2) ] = √3 .
x = π / 3+ πn , n ∈ ℤ. откуда появился второй корень
task/29453615
Вычислить : sin( arcsin 8/15 - arcsin 8/17 )
α = arcsin 8 / 15 ; β = arcsin 8/17
sin(arcsin8/15)*cos(arcsin8/17) - cos(arcsin8/15) *sin(arcsin8/17)=
* * *cosα= √(1 -(8/15)² ) =√(1 -64/225 ) =√(161/225 ) =(√161) /15 * * *
* * *cosβ= √(1 -(8/17)² ) =√(1 -64/289 ) =√(225/289 ) = 15 /17 * * *
sin(arcsin8/15)*cos(arccos(15 /17) - cos(arccos(√161) /15) *sin(arcsin8/17) =
8/15*15 /17 - (√161) /15 ) * 8/17 = (8/17)*(1 - (√161) /15 ).
1)х^4+6x^2y+9y^2
2)((0,3)^2+4b)^2
3)одна двадцать пятая m^4-2m^2n+25n^2
4)сто шестдесят девять сотых p ^6+ тринадцать вторых p^5+двадцать пять четвертыхp^4
5)cто сорок четыре двадцать пятых c^6- тридцать шесть пятых c^3d^2+девять четвертых d^4
6)49x^4y^2+42x^3y^3+9x^2y^4