Завдання 1:
Координати точки, яка належить графіку функції (або через яку проходить графік), будуть задовільняти формулу, якою ця функція задана.
Підставимо координати точки В (-2; у) у формулу: абсцису замість х, ординату замість у.
у = -3 ∙ (-2).
Тепер можемо обчислити ординату:
у = 6.
Відповідь: 6.
Завдання 2:
Підставимо координати точки N (-4; 9) у формулу: : абсцису замість х, ординату замість у.
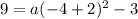
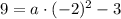
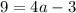
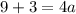
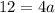
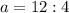
a = 3.
Відповідь: 3.
Завдання 3:
Щоб вирішити рівняння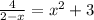 
графічно, треба побудувати графіки двох функцій:
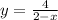та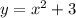 
.
Коренями рівняння будуть абсциси точок перетину цих графіків.
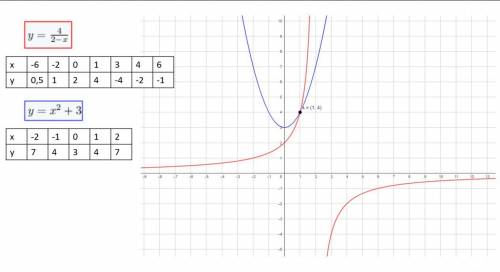
Побудуємо графіки, створивши таблицю точок, що належать їм (див. малюнок).
Точка перетину графіків А (1;4).
х = 1.
Відповідь: 1.
у = х² - 4х + 3
а) Ограничений нет, D(y) = (-беск; +беск).
b) у = х² - 4х + 3
х² - 4х + 3 = 0
(х - 1)(х - 3) = 0 (по теореме Виета)
Произведение равно нулю, если хотя бы один из множителей равен нулю => либо (х-1), либо (х-3) равно нулю => нули функции: 1 и 3 (это и есть ответ).
с) y = x² - 4x + 3
y' = 2x - 4 - уравнение линейное => у функции есть толь один экстремум
y'' = 2 => у функции есть только минимум, который нам и нужен
2х - 4 = 0
2х = 4
х = 2
у(2) = 2² - 4*2 + 3 = 4 - 8 + 3 = -1
ответ: -1.
При n=4 неравенство верное
3^4>4^3+5 (верно)
при k=n+1
3^n*3>(n+1)^3+5
3*3^n>n^3+3n^2+3n+6
Из того что 3^n>n^3+5
откуда
2*3^n>3n^2+3n+1
2*3^n>2*(n^3+5)>3n^2+3n+1
Требуется доказать
2(n^3+5)>3n^2+3n+1
(2n+3)(n^2-3n+3)>0
Так как n^2-3n+3>=0
При всех n>=0
То 2n+3>0 при n>=4
Откуда следует верность неравенства