1) х принадлежит (-бесконечность, 1] или [ 2,1+sqrt(3))
2) х принадлежит
(-бесконечность, 2-sqrt(5)) или (2+sqrt(5),+бесконечность)
Объяснение:
1) ОДЗ: x^2-x-2>=0
При этом условии х>x^2-x-2
3>x^2-2x+1
3>(x-1)^2
1-sqrt(3) <x<1+sqrt(3)
Вернемся к ОДЗ
(x-0,5)^2>=1,5^2
x>=2 или x<=-1
Из пересечения областей решений и ОДЗ вытекает
х x<=-1 или 2=<x<1+sqrt(3)
х принадлежит (-бесконечность, 1] или [ 2,1+sqrt(3))
2) ОДЗ
x^2-3x+2 >=0
x^2-3x+2,25 >=0,5^2
x>=2 или x<=1
тогда
x^2-3x+2 >х+3
x^2-4x+4 >5
x>=2+sqrt(5) или х=<2-sqrt(5)
х принадлежит
(-бесконечность, 2-sqrt(5)) или (2+sqrt(5),+бесконечность)
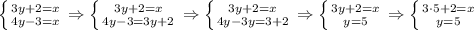
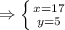
7ab - 7b + 5ab + a^2 - 2b = a^2 + 12ab - 2ab
3c^3-d^2-5cd+4cd-c^3-7d^2 = 2c^3-8d^2-cd
7x(-42x^3+28x-12x^2+8) = -294x^4 + 196x^2 - 84x^3 + 56x