6. (a — 5x)² + (a + 5x²) = a² —10ax + 25x² + a + 5x² = a² + a — 10ax + 30x² = a(a + 1) — 10x(a + 3x); И всё же мне кажется, что ты допустила ошибку в написании данного выражение, поэтому держи альтернативный вариант решения на всякий случай (если ты, конечно, допустила ошибку): (a — 5x)² + (a + 5x)² = (a — 5x + a + 5x)(a — 5x — a — 5x) = 2a * (—10x) = —20ax;
Пусть первая машинистка может выполнить работу за Х дней, тогда по условию вторая может выполнить эту же работу за Х +15 дней
Учитывая, что производительность совместной работы равна сумме производительностей каждого участника работы, составим таблицу: ______________________________________________________ Работа Производительность Время ______________________________________________________ I маш. 1 1/ Х Х ______________________________________________________ II маш. 1 1/ (Х+15) Х + 15 ______________________________________________________ I +II маш. 1 1/ Х + 1/ (Х+15) 10 ______________________________________________________
Из последней строки следует уравнение:
По теореме Виета: х1+х2 = 5, х1*х2 = -150 => х1 = 15, х2= - 10 Второй корень не подходит, т.к. время не может быть отрицательным.
Значит Х = 15 (время первой машинистки - 15 дней). Тогда вторая машинистка выполнит эту же работу за Х+15 = 15+15 = 30 дней..
Составим систему и определим значения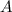 и
и 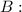
Высчитываем выражение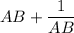 , подставляя значения букв
, подставляя значения букв 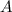 и
и 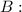
ответ: 54.