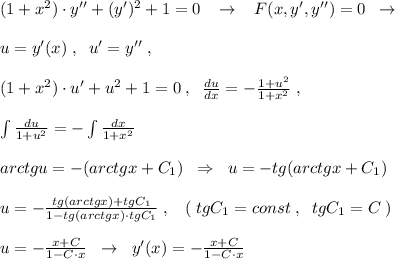
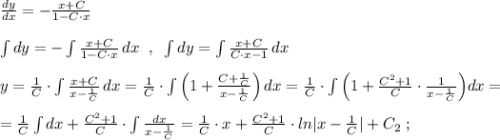
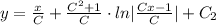
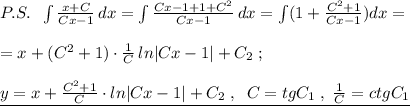
ответ:Чтобы разложить данные выражения на множители, надо преобразовать их в произведения, используя при этом формулы сокращенного умножения;
1) аb - 3 b + b^2 - 3 a, применим группировки;
(a b + b2) - (3 b + 3 a), из каждой скобки вынесем общий множитель;
b * (a + b) - 3 * ( b + a), теперь вынесем общий множитель выражения;
(a + b) * (b - 3).
2) 11 х - х у + 11 y - х^2, аналогично решению предыдущего примера, разложим на множители следующие выражения;
(11 x + 11 y) - (x^2 + x y) = 11 * (x + y) - x * (x + y) = (x + y) * (11 - x)
3) k n - m n - n^2 + m
Объяснение:
Задача 2:
2) В двух коробках b карандашей, причём в первой коробке в 4 раза больше...
(b -4) / 2
Задача 3:
3) В двух коробках c карандашей, причём во второй коробке на 12 карандашей...
Пусть x (карандашей) - в первой коробке, тогда во второй коробке (x - 12) (карандашей), по условию задачи всего C карандашей, составим уравнение:
x + (x - 12) = C
x + x - 12 = C
2x = C + 12 (если вопрос:"А ПОЧЕМУ СТАЛО С+12?", то знайте при переносе числа из одной стороны в другую знак меняется)
x = (C +12) / 2
и с лёгкостью находим икс
Задача 1:
1) Периметр прямоугольника 24 см, одна его сторона в 5 раз больше другой...
Пусть x - одна сторона, тогда 5*x другая сторона, по условию задачи известно что периметр их равен 24 ;общая формула периметра P = (a+b) * 2, составим уравенение:
( x + 5x ) * 2 = 24
2x + 10x = 24
12x = 24
x = 24 / 12
x = 2(см) (первую сторону нашли)
вторая сторона равна 5x, значит 5 * 2 = 10(см)
Формула площади a * b
2 * 10 = 20()
Понизим порядок заменой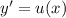 , тогда
, тогда 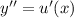 , получим
, получим
Выполнив обратную замену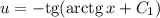 , получим
, получим
Тогда