Алгебра: Представьте в виде дроби. (8класс) заранее !

выпишем координаты данных векторов:a)координаты:скалярное произведение векторов - число:б)координаты:векторное произведение векторов - вектор, находим его координаты:находим модуль(длину) полученного вектора:в)координаты:смешанное произведение векторов - число, находим его:г)Координаты:Векторы коллинеарны, если их соответствующие кординаты пропорциональныПроверим это утверждение:Данное равенство неверно, значит векторы b и c не коллинеарныВекторы ортогональны, если их скалярное произведение равно...

Представьте в виде дроби. (8класс)
заранее !

👇

Увидеть ответ

Ответ:

киска555555544

30.03.2022

ответ:

$2 \frac{85}{..455? }$

4,4(25 оценок)

Открыть все ответы

Ответ:

GrinnySmith

30.03.2022

1) 11х = 36 - х

ОДЗ уравнения:

x ∈ ( -∞, ∞)

Делаем преобразование правой части уравнения:

36 - x = - ( x - 36)

Уравнение после преобразования:

11x = - (x - 36)

Упрощаем:

12x = 36

Сокращаем:

12(убираем)x = 12(убираем) * 3

x=3

2) 9х + 4 = 48 - 2х

ОДЗ уравнения:

x ∈ ( -∞, ∞)

Делаем преобразование правой части уравнения:

48 - 2x = -2 * (x - 24)

Уравнение после преобразования:

9x + 4 = -2 * (x - 24)

Упрощаем:

11x = 44

Сокращаем:

11(убираем)x = 11(убираем) * 4

x=4

3) 8 - 4х = 2х - 16

ОДЗ уравнения:

x ∈ ( -∞, ∞)

Делаем преобразование левой части уравнения:

8 - 4x = -4 * (x - 2)

Делаем преобразование правой части уравнения:

2x - 16 = 2 * (x - 8)

Уравнение после преобразования:

-4 * (x - 2) = 2 * (x - 8)

Упрощаем:

-6x = -24

Сокращаем:

-6(убираем)x = -6(убираем) * 4

x = 4

За остальным, если желаешь - в ЛС.

4,7(70 оценок)

Ответ:

milankae

30.03.2022

выпишем координаты данных векторов:

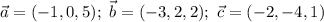
$\vec{a}=(-1,0,5);\ \vec{b}=(-3,2,2);\ \vec{c}=(-2,-4,1)$

координаты:

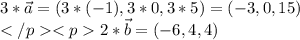
$3*\vec{a}=(3*(-1),3*0,3*5)=(-3,0,15)\\2*\vec{b}=(-6,4,4)$

скалярное произведение векторов - число:

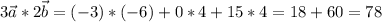
$3\vec{a}*2\vec{b}=(-3)*(-6)+0*4+15*4=18+60=78$

б)

координаты:

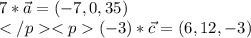
$7*\vec{a}=(-7,0,35)\\(-3)*\vec{c}=(6,12,-3)$

векторное произведение векторов - вектор, находим его координаты:

$7\vec{a}\times (-3\vec{b})=\left|\begin{array}{ccc}\vec{i} & \vec{j} & \vec{k} \\-7 & 0 & 35 \\6 & 12 & -3\end{array}\right|=\vec{i}*\left|\begin{array}{cc}0 & 35 \\12 & -3\end{array}\right|-\vec{j}*\left|\begin{array}{cc}-7 & 35 \\6 & -3\end{array}\right|+\vec{k}*\left|\begin{array}{cc}-7 & 0 \\6 & 12\end{array}\right|=\vec{i}*(-12*35)-\vec{j}*(21-6*35)+\vec{k}*(12*(-7))=\\=-420\vec{i}+189\vec{j}-84*\vec{k}=(-420,189,-84)$

находим модуль(длину) полученного вектора:

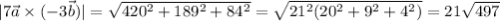
$|7\vec{a}\times (-3\vec{b})|=\sqrt{420^2+189^2+84^2}=\sqrt{21^2(20^2+9^2+4^2)}=21\sqrt{497}$

в)

координаты:

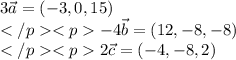
$3\vec{a}=(-3,0,15)\\-4\vec{b}=(12,-8,-8)\\2\vec{c}=(-4,-8,2)$

смешанное произведение векторов - число, находим его:

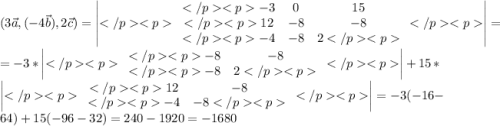
$(3\vec{a},(-4\vec{b}),2\vec{c})=\left|\begin{array}{ccc}-3 & 0 & 15 \\12 & -8 & -8 \\-4 & -8 & 2\end{array}\right|=\\=-3*\left|\begin{array}{cc}-8 & -8 \\-8 & 2\end{array}\right|+15*\left|\begin{array}{cc}12 & -8 \\-4 & -8\end{array}\right|=-3(-16-64)+15(-96-32)=240-1920=-1680$

г)

Координаты:

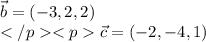
$\vec{b}=(-3,2,2)\\\vec{c}=(-2,-4,1)$

Векторы коллинеарны, если их соответствующие кординаты пропорциональны

Проверим это утверждение:

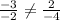
$\frac{-3}{-2}\neq \frac{2}{-4}$

Данное равенство неверно, значит векторы b и c не коллинеарны

Векторы ортогональны, если их скалярное произведение равно нулю.

Проверим это утверждение:

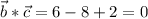
$\vec{b}*\vec{c}=6-8+2=0$

- верно, значит данные векторы ортогональны

Векторы b и c ортогональны

д)

Координаты:

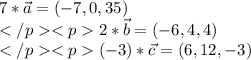
$7*\vec{a}=(-7,0,35)\\2*\vec{b}=(-6,4,4)\\(-3)*\vec{c}=(6,12,-3)$

Три вектора компланарны, если их смешанное произведение равно нулю.

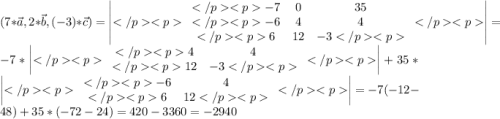
$(7*\vec{a},2*\vec{b},(-3)*\vec{c})=\left|\begin{array}{ccc}-7 & 0 & 35 \\-6 & 4 & 4 \\6 & 12 & -3\end{array}\right|=-7*\left|\begin{array}{cc}4 & 4 \\12 & -3\end{array}\right|+35*\left|\begin{array}{cc}-6 & 4 \\6 & 12\end{array}\right|=-7(-12-48)+35*(-72-24)=420-3360=-2940$