Для начала вспомним, что тупой угол - это угол с градусной мерой больше 90° и меньше 180°. Из одной точки можно пустить три луча, которые между собой образуют 3 тупых угла.
Пустим 4-й луч вблизи одного из трёх лучей, у нас добавится дополнительно 2 тупых угла. 5-й луч пустим вблизи второго из числа первых трёх, дополнительно образуются 3 тупых угла. Наконец, пускаем 6-й луч вблизи третьего, получив дополнительно 4 тупых угла. У нас будет получаться как бы три пучка близко расположенных лучей в каждом пучке.
Считаем сколько получилось тупых углов после добаления к первым трём лучам ещё трёх лучей. 3 луча было, плюс 2, плюс 3 и плюс 4, всего 12 лучей.
Итак, для 3-х лучей - 3 тупых угла; для 6 лучей - 12 тупых углов.
Рассуждаем аналогично, добавляя по очереди ещё 3 луча. Добавятся сначало 4 угла, затем 5 и, наконец, 6; т.е. всего добавится 15 тупых углов. А всего для 9 лучей будет 27 тупых углов.
Точно также, считая для 12 лучей, получим дополнительно 6+7+8 = 21 тупых угла, а всего - 48.
Можно было бы и далее продолжать таким но мы замечаем закономерность.
Пусть а1 = 3 - это первый член последовательности. Используя предыдущее значение (рекуррентно), можно вычислить следующее значение по формуле: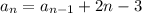 , где n - число лучей кратное 3.
, где n - число лучей кратное 3.
Пробуем вычислить по этой формуле:

Итак, ответ найден. Для 27 лучей возможно максимум 243 тупых угла.
Так считать долго, можно увидеть формулу для прямого расчёта: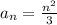
По этой формуле можно считать для любого количества лучей, кратное трём.
нет
Объяснение:
2x² +2x +1 -7y² = 2007 ⇔ 2x²+2x -2006 = 7y² ( 1 )
так как левая часть равенства ( 1 ) - четное число , то и правая
часть кратна 2 ⇒ 7y² делится на 2 ⇒ y делится на 2 ⇒
y = 2k ; k∈Z , подставим в (1) вместо y число 2к :
2x²+2x -2006 =28k² ⇒ x²+x -14k² = 1003 или :
x(x+1) -14k² = 1003 ( 2 )
x и ( x +1 ) - 2 последовательных натуральных числа ⇒ одно
из них обязательно четно ⇒ x(x+1) - четно ⇒ x(x+1) -14k² - четно
, как разность двух четных чисел , но 1003 - нечетное число
⇒ равенство ( 2) невозможно ⇒ уравнение (1) не имеет
решений в целых числах
Пусть х - скорость по расписанию
Тогда
420/(х+10) + 1 = 420/х
(420+х+10)/(х+10) = 420/х
420х+х²+10х = 420х+4200
х²+10х-4200 = 0
(х-60)(х+70) = 0
Скорость поезда положительная, следовательно
х = 60