Найдите наименьшее пятизначное число, кратное 55, произведение цифр которого больше 50, но меньше 75.

👇

Ответ:

olya2399

07.10.2021

Число делится на 55 если оно делится и на 5 и на 11. По признаку делимости на 5, число делится на 5 тогда, когда его последняя цифра 0 или 5, но так как если последняя цифра будет 0, то произведение цифр пятизначных чисел будет 0, поэтому последняя цифра будет 5.

Для удобства назовем наше число abcde, где каждая буква обозначает конкретный разряд числа: a – десятки тысяч, b – тысячи, c – сотни, d – десятки и e – единицы.

Число делится на 11, если сумма цифр на нечётных местах равна сумме цифр на чётных местах:

$a+c+e=b+d~~~\Leftrightarrow~~~a+c+5=b+d$

По условию задачи: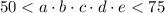 . Возможные значения произведения пятизначного числа : 55, 60, 65, 70 и разложим каждое число на простые множители

55 = 5 * 11

60 = 2 * 2 * 3 * 5

65 = 5 * 13

70 = 2 * 5 * 7

Перебираем возможные варианты составить числа и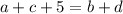 a+c+5=b+d

6, 5, 2, 1, 1 разбить никак

5, 4, 3, 1, 1: 5 + 1 + 1 = 4 + 3; ⇒ 14135, 13145

5, 3, 2, 2, 1 разбить никак

7, 5, 2, 1, 1: 5 + 2 + 1 = 7 + 1; ⇒ 27115, 21175, 17215, 11275

Отсюда наименьшее 11 275; $\overline{abcde}=1\cdot 1\cdot 2\cdot 5\cdot 7$

ответ: 11 275.

4,5(79 оценок)

Открыть все ответы

Ответ:

vladiktikhonov2

07.10.2021

Удобнее всего решать эту задачу, используя единицы измерения скорости – км/мин. А в конце все полученные результаты перевести в км/ч.

Пусть скорость медленного гонщика составляет

км/мин.

Раз быстрый гонщик обогнал впервые медленного через 48 минут, то с таким же успехом, мы можем переформулировать это утверждение и так: быстрый гонщик через 48 минут опережал медленного на 8 км (длину одного круга). А значит, их относительная скорость удаления составляет: 8 : 48 = 1/6

км/мин.

Из найденного следует, что скорость быстрого гонщика мы можем записать, как: ( x + 1/6 )

км/мин.

Сказано, что медленный гонщик ехал на 17 минут дольше, а значит, если мы вычтем из времени в пути медленного гонщика время в пути быстрого гонщика, то эта разность и должна составить 17 минут. Ясно, что время в пути для каждого гонщика мы можем найти, разделив полный путь трассы на скорость каждого из них, тогда:

$\frac{ 85 \cdot 8 }{x} - \frac{ 85 \cdot 8 }{ x + 1/6 } = 17 \ ;$

$\frac{ 85 \cdot 8 }{x} - \frac{ 85 \cdot 8 }{ x + 1/6 } = 17 \ ; \ \ \ || : 17$

$\frac{ 5 \cdot 8 }{x} - \frac{ 5 \cdot 8 }{ x + 1/6 } = 1 \ ;$

$\frac{ 5 \cdot 8 }{x} - \frac{ 5 \cdot 8 }{ x + 1/6 } = 1 \ ; \ \ \ || : 40$

$\frac{1}{x} - \frac{1}{ x + 1/6 } = \frac{1}{40} \ ;$

$\frac{ x + 1/6 }{ x ( x + 1/6 ) } - \frac{x}{ x ( x + 1/6 ) } = \frac{1}{40} \ ;$

$\frac{ ( x + 1/6 ) - x }{ x^2 + x/6 } = \frac{1}{40} \ ;$

$\frac{ x + 1/6 - x }{ x^2 + x/6 } = \frac{1}{40} \ ; \ \ \ || \cdot ( x^2 + x/6 )$

$\frac{1}{6} = \frac{ x^2 + x/6 }{40} \ ;$

$\frac{1}{6} = \frac{ x^2 + x/6 }{40} \ ; \ \ \ || \cdot 120$

$20 = 3 \cdot ( x^2 + x/6 ) \ ;$

$20 = 3 \cdot ( x^2 + x/6 ) \ ; \ \ \ || \cdot 2$

$40 = 6x^2 + x \ ;$

$6x^2 + x - 40 = 0 \ ;$

$D = 1^2 - 4 \cdot 6 \cdot (-40) = 1 + 24 \cdot 40 = 1 + 960 = 900 + 61 = 30^2 + 30 + 31 = 31^2 \ ;$

$x \in \frac{ -1 \pm 31 }{ 2 \cdot 6 } \ ;$

Поскольку $x 0 \ ,$ так, как это скорость,
направленная в заданную сторону (вперёд), то:

$x = \frac{ -1 + 31 }{ 2 \cdot 6 } = \frac{30}{ 2 \cdot 6 } = \frac{15}{6} \ ;$

Это и есть скорость второго (медленного) гонщика.
Осталось только перевести её в км/ч:

15/6 км/мин = 15 км : 6 мин = 150 км : 60 мин = 150 км : час = 150 км/час.

О т в е т : 150 км.

4,8(74 оценок)

Ответ: